Giải Toán 12 trang 51 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 12 trang 51 Tập 2 trong Bài 16: Công thức tính góc trong không gian Toán 12 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 51.

Giải Toán 12 trang 51 Tập 2 Kết nối tri thức

Luyện tập 1 trang 51 Toán 12 Tập 2: Trong không gian Oxyz, tính góc giữa trục Oz và đường thẳng $\Delta :\frac{x-3}{1}=\frac{y+1}{2}=\frac{z-1}{-2}$

Lời giải:

Trục Oz có vectơ chỉ phương là $\overrightarrow{k}=\left(0;0;1\right)$

Đường thẳng ∆ có vectơ chỉ phương là $\overrightarrow{u}=\left(1;2;-2\right)$

Khi đó $\cos \left(Oz,\Delta \right)=\left|\cos \left(\overrightarrow{k},\overrightarrow{u}\right)\right|=\frac{\left|-2\right|}{\sqrt{1^2}.\sqrt{1^2+2^2+{\left(-2\right)}^2}}=\frac{2}{3}$

Vậy (Oz, ∆) ≈ 48,2°.

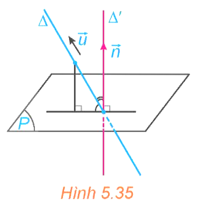
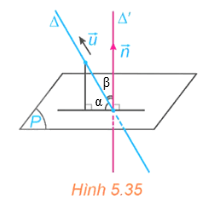
HĐ2 trang 51 Toán 12 Tập 2: Trong không gian Oxyz, cho đường thẳng ∆ và mặt phẳng (P). Xét $\overrightarrow{u}=\left(a;b;c\right)$ là một vectơ chỉ phương của ∆ và $\overrightarrow{n}=\left(A;B;C\right)$ (với giá ∆') là một vectơ pháp tuyến của (P). (H.5.35)

a) Hãy tìm mối quan hệ giữa các góc (∆, (P)) và (∆, ∆').

b) Có nhận xét gì về mối quan hệ giữa sin(∆, ∆') và $\left|\cos \left(\overrightarrow{u},\overrightarrow{n}\right)\right|$?

Lời giải:

a) Gọi α = (∆, (P)), β = (∆, ∆').

Có α + β = 90°. Suy ra (∆, ∆') = 90° − (∆, (P)).

b) Có sin(∆, ∆') $=\left|\cos \left(\overrightarrow{u},\overrightarrow{n}\right)\right|$.

Luyện tập 2 trang 51 Toán 12 Tập 2: Trong không gian Oxyz, tính góc giữa đường thẳng ∆ và mặt phẳng (P), với: $\Delta :\frac{x+2}{-1}=\frac{y-4}{2}=\frac{z+1}{1}$, (P): x – y + z – 1 = 0.

Lời giải:

Đường thẳng ∆ có vectơ chỉ phương là $\overrightarrow{u}=\left(-1;2;1\right)$

Mặt phẳng (P) có vectơ pháp tuyến là $\overrightarrow{n}=\left(1;-1;1\right)$

Ta có $\sin \left(\Delta ,\left(P\right)\right)=\frac{\left|-1-2+1\right|}{\sqrt{{\left(-1\right)}^2+2^2+1^2}.\sqrt{1^2+{\left(-1\right)}^2+1^2}}=\frac{2}{3\sqrt{2}}$

Do đó (∆, (P)) ≈ 28,1°.

Lời giải bài tập Toán 12 Bài 16: Công thức tính góc trong không gian hay khác:

• Giải Toán 12 trang 50
• Giải Toán 12 trang 52
• Giải Toán 12 trang 53