Giải Toán 12 trang 52 Tập 2 Kết nối tri thức

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 12 trang 52 Tập 2 trong Bài 16: Công thức tính góc trong không gian Toán 12 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 52.

Giải Toán 12 trang 52 Tập 2 Kết nối tri thức

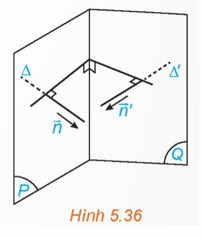
HĐ3 trang 52 Toán 12 Tập 2: Trong không gian Oxyz, cho hai mặt phẳng (P), (Q) tương ứng có các vectơ pháp tuyến là $\overrightarrow{n}=\left(A;B;C\right)$, $\overrightarrow{n^{\text{'}}}=\left(A^{\text{'}};B^{\text{'}};C^{\text{'}}\right)$. Lấy các đường thẳng ∆, ∆' tương ứng có vectơ chỉ phương $\overrightarrow{n},\overrightarrow{n^{\text{'}}}$. (H.5.36)

a) Góc giữa hai mặt phẳng (P) và (Q) và góc giữa hai đường thẳng ∆ và ∆' có mối liên hệ gì?

b) Tính côsin của góc giữa hai mặt phẳng (P) và (Q).

Lời giải:

a) Đường thẳng ∆, ∆' tương ứng có vectơ chỉ phương $\overrightarrow{n},\overrightarrow{n^{\text{'}}}$ nên ∆ ⊥ (P) và ∆' ⊥ (Q).

Do đó ((P), (Q)) = (∆, ∆').

b) Có $\cos \left(\left(P\right),\left(Q\right)\right)=\cos \left(\Delta ,{\Delta }^{\text{'}}\right)=\left|\cos \left(\overrightarrow{n},\overrightarrow{n^{\text{'}}}\right)\right|$

Luyện tập 3 trang 52 Toán 12 Tập 2: Trong không gian Oxyz, tính góc giữa hai mặt phẳng (P): $x-\sqrt{2}y+z-2=0$ và (Oxz): y = 0.

Lời giải:

Mặt phẳng (P) có vectơ pháp tuyến $\overrightarrow{n}=\left(1;-\sqrt{2};1\right)$

Mặt phẳng (Oxz) có vectơ pháp tuyến $\overrightarrow{n^{\text{'}}}=\left(0;1;0\right)$

Có $\cos \left(\left(P\right),\left(Oxz\right)\right)=\frac{\left|1.0-\sqrt{2}.1+1.0\right|}{\sqrt{1+2+1}.\sqrt{1}}=\frac{\sqrt{2}}{2}$

Suy ra ((P), (Oxz)) = 45°.

Lời giải bài tập Toán 12 Bài 16: Công thức tính góc trong không gian hay khác:

• Giải Toán 12 trang 50
• Giải Toán 12 trang 51
• Giải Toán 12 trang 53