Toán lớp 5 Bài 71: Ôn tập hình học - Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán lớp 5 Bài 71: Ôn tập hình học sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán lớp 5.

Giải Toán lớp 5 Bài 71: Ôn tập hình học - Kết nối tri thức

Toán lớp 5 trang 113, 114 Tập 2 Luyện tập

Giải Toán lớp 5 trang 113 Tập 2

Giải Toán lớp 5 Tập 2 trang 113 Bài 1:

a) Hoàn thành công thức tính chu vi, diện tích hình chữ nhật, hình vuông.

P = ( + ) × 2 S = ×

P = × 4 S = ×

b) Số?

Một mảnh vườn trồng hoa dạng hình vuông có cạnh 60 m, một mảnh vườn trồng rau dạng hình chữ nhật có chiều dài gấp đôi chiều rộng. Biết chu vi của hai mảnh vườn bằng nhau.

- Diện tích mảnh vườn trồng hoa là cm².

- Diện tích mảnh vườn trồng rau là cm².

Lời giải:

a)

P = (a + b) × 2 S = a × b

P = a × 4 S = a × a

b)

- Diện tích mảnh vườn trồng hoa là 3 600 cm².

- Diện tích mảnh vườn trồng rau là 3 200 cm².

Giải thích:

Diện tích mảnh vườn trồng hoa là: 60 × 60 = 3 600 (cm²)

Chu vi mảnh vườn trồng hoa là: 60 × 4 = 240 (cm)

Nửa chu vi mảnh vườn trồng rau là: 240 : 2 = 120 (cm)

Chiều dài mảnh vườn trồng rau là: 120 : (2 + 1) × 2 = 80 (cm)

Chiều rộng mảnh vườn trồng rau là: 120 – 80 = 40 (cm)

Diện tích mảnh vườn trồng rau là: 80 × 40 = 3 200 (cm²)

Giải Toán lớp 5 Tập 2 trang 113 Bài 2:

a) Hoàn thành công thức tính diện tích hình tam giác, hình thang.

b) Số?

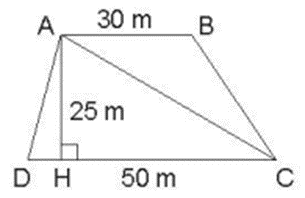
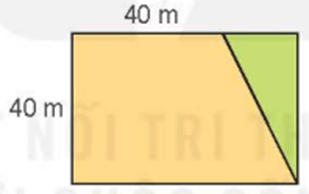
Có một mảnh đất dạng hình thang với kích thước như hình bên.

- Diện tích mảnh đất hình tam giác ACD là m².

- Diện tích mảnh đất hình thang ABCD là m².

Lời giải:

a)

b)

- Diện tích mảnh đất hình tam giác ACD là 625 m².

- Diện tích mảnh đất hình thang ABCD là 1 000 m².

Giải thích:

Diện tích mảnh đất hình tam giác ACD là: $\frac{50\times 25}{2}$ = 625 (m²)

Diện tích mảnh đất hình thang ABCD là: $\frac{(50+30)\times 25}{2}$ = 1 000 (m²)

Giải Toán lớp 5 trang 114 Tập 2

Giải Toán lớp 5 Tập 2 trang 114 Bài 3:

a) Hoàn thành công thức tính chu vi, diện tích hình tròn.

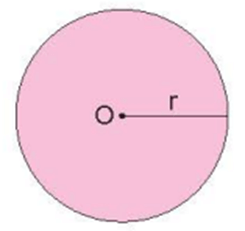C = 3,14 × × 2 S = 3,14 × ×

b) Số?

Một đĩa sứ trang trí có dạng hình tròn đường kính 24 cm.

- Chu vi đĩa sứ là cm.

- Diện tích đĩa sứ là cm².

Lời giải:

a)

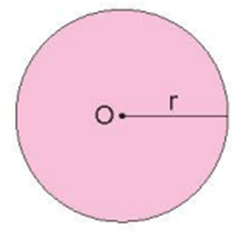C = 3,14 × r × 2 S = 3,14 × r × r

b)

- Chu vi đĩa sứ là 75,36 cm.

- Diện tích đĩa sứ là 452,16 cm².

Giải thích:

Chu vi đĩa sứ là: 3,14 × 24 = 75,36 (cm)

Bán kính đĩa sứ là: 24 : 2 = 12 (cm)

Diện tích đĩa sứ là: 3,14 × 12 × 12 = 452,16 (cm²)

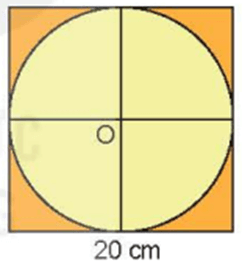
Giải Toán lớp 5 Tập 2 trang 114 Bài 4: Từ miếng bìa hình vuông cạnh 20 cm, Mai muốn cắt ra một hình tròn to nhất có thể. Rô-bốt đã giúp Mai cắt được hình tròn như hình bên.

a) Tính chu vi miếng bìa hình tròn.

b) Tính diện tích phần bìa còn lại ở hình vuông.

Lời giải:

a) Chu vi miếng bìa hình tròn là: 3,14 × 20 = 62,8 (cm)

b) Diện tích miếng bìa hình vuông là: 20 × 20 = 400 (cm²)

Bán kính hình tròn là: 20 : 2 = 10 (cm)

Diện tích hình tròn là: 3,14 × 10 × 10 = 314 (cm²)

Diện tích phần bìa còn lại ở hình vuông là: 400 – 314 = 86 (cm²)

Đáp số: a) 62,8 cm

b) 86 cm².

Toán lớp 5 trang 114, 115 Tập 2 Luyện tập

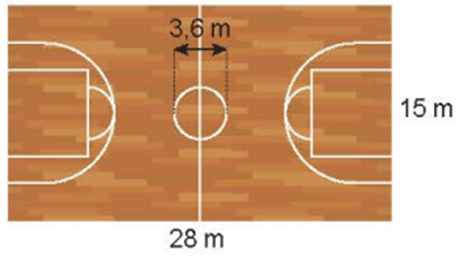
Giải Toán lớp 5 Tập 2 trang 114 Bài 1: Một sân bóng rổ dạng hình chữ nhật có kích thước như hình vẽ dưới đây.

a) Tính chu vi và diện tích sân bóng rổ.

b) Tính chu vi và diện tích hình tròn ở giữa sân bóng rổ.

Lời giải:

a) Chu vi sân bóng rổ là:

(28 + 15) × 2 = 86 (m)

Diện tích sân bóng rổ là:

28 × 15 = 420 (m²)

Đáp số: Chu vi: 86 m

Diện tích: 420 m²

b) Chu vi hình tròn giữa sân bóng rổ là:

3,14 × 3,6 = 11,304 (m)

Bán kính hình tròn giữa sân bóng rổ là:

3,6 : 2 = 1,8 (m)

Diện tích hình tròn giữa sân bóng rổ là:

3,14 × 1,8 × 1,8 = 10,1736 (m²)

Đáp số: Chu vi: 11,304 m

Diện tích: 10,1736 m²

Giải Toán lớp 5 trang 115 Tập 2

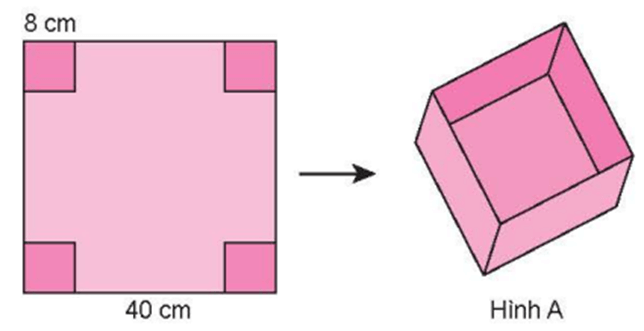
Giải Toán lớp 5 Tập 2 trang 115 Bài 2: Từ miếng bìa hình vuông cạnh 40 cm, Nam đã cắt 4 hình vuông cạnh 8 cm ở bốn góc, rồi gấp lên để được cái hộp không nắp (hình A). Tính diện tích miếng bìa làm thành cái hộp hình A đó.

Lời giải:

Diện tích miếng bìa ban đầu là:

40 × 40 = 1 600 (cm²)

Diện tích 4 hình vuông đã cắt là:

(8 × 8) × 4 = 256 (cm²)

Diện tích miếng bìa làm thành cái hộp hình A là:

1 600 – 256 = 1 344 (cm²)

Đáp số: 1 344 cm².

Giải Toán lớp 5 Tập 2 trang 115 Bài 3: Một khu đất dạng hình thang vuông có chiều cao bằng đáy bé và bằng 40 m, độ dài đáy lớn bằng $\frac{3}{2}$ đáy bé. Để xây dựng khu nhà văn hoá, đội xây dựng đã cải tạo, đắp đất mở rộng khu đất cũ thành khu đất mới dạng hình chữ nhật có chiều rộng bằng chiều cao hình thang, có chiều dài bằng đáy lớn hình thang (như hình vẽ).

a) Tính diện tích khu đất dạng hình thang ban đầu.

b) Tính diện tích phần đất được mở rộng.

Lời giải:

a) Độ dài đáy lớn là:

40 × $\frac{3}{2}$ = 60 (m)

Diện tích khu đất dạng hình thang ban đầu là:

(40 + 60) × 40 : 2 = 2 000 (m²)

b) Diện tích khu đất mới là:

40 × 60 = 2 400 (m²)

Diện tích phần đất được mở rộng là:

2 400 – 2 000 = 400 (m²)

Đáp số: 400 m².

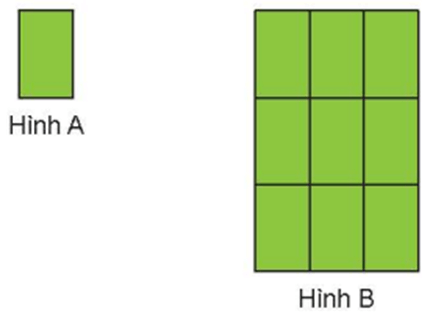
Giải Toán lớp 5 Tập 2 trang 115 Bài 4: Số?

Việt cắt 9 tờ giấy màu, mỗi tờ là hình chữ nhật có chu vi 30 cm (hình A). Việt đã dán 9 tờ giấy màu đó thành hình chữ nhật (hình B).

a) Chu vi hình B là cm.

b) Nếu hình chữ nhật B có chiều dài hơn chiều rộng 9 cm thì diện tích hình A là cm².

Lời giải:

a) Chu vi hình B là 90 cm.

b) Nếu hình chữ nhật B có chiều dài hơn chiều rộng 9 cm thì diện tích hình A là 54 cm².

Giải thích:

a) Tổng chiều rộng và chiều dài của hình chữ nhật A là: 30 : 2 = 15 (cm)

Dựa vào hình B ta thấy, chu vi hình B gấp 6 lần tổng chiều rộng và chiều dài của hình chữ nhật A.

Chu vi hình chữ nhật B là: 15 × 6 = 90 (cm)

b) Nửa chu vi hình B là: 90 : 2 = 45 (cm)

Chiều dài hình B là: (45 + 9) : 2 = 27 (cm)

Chiều rộng hình B là: 27 – 9 = 18 (cm)

Diện tích hình B là: 27 × 18 = 486 (cm²)

Diện tích hình A là: 486 : 9 = 54 (cm²)

Toán lớp 5 trang 116, 117 Tập 2 Luyện tập

Giải Toán lớp 5 trang 116 Tập 2

Giải Toán lớp 5 Tập 2 trang 116 Bài 1: Hoàn thành công thức tính diện tích và thể tích hình hộp chữ nhật, hình lập phương.

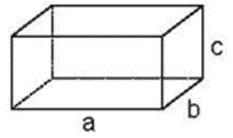	Sxung quanh = (a + b) × 2 × Stoàn phần = Sxung quanh + Sđáy × V = a × b ×
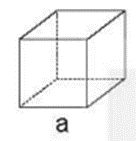	Sxung quanh = a × a × Stoàn phần = × × 6 V = × ×

Lời giải:

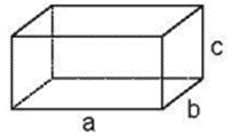	Sxung quanh = (a + b) × 2 × c Stoàn phần = Sxung quanh + Sđáy × 2 V = a × b × c
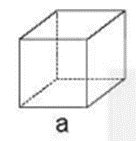	Sxung quanh = a × a × 4 Stoàn phần = a × a × 6 V = a × a × a

Giải Toán lớp 5 Tập 2 trang 116 Bài 2:

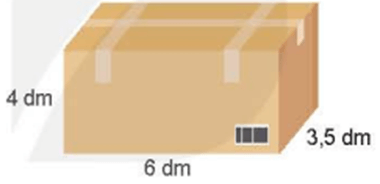
a) Tính diện tích xung quanh và diện tích toàn phần một thùng hàng dạng hình hộp chữ nhật với kích thước như hình bên.

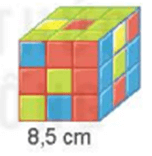
b) Tính diện tích xung quanh và diện tích toàn phần một khối ru-bích hình lập phương có cạnh 8,5 cm.

Lời giải:

a) Diện tích xung quanh của thùng hàng là: (6 + 3,5) × 2 × 4 = 76 (dm²)

Diện tích toàn phần của thùng hàng là: 76 + 6 × 3,5 × 2 = 118 (dm²)

b) Diện tích xung quanh của khối ru-bích là: 8,5 × 8,5 × 4 = 289 (cm²)

Diện tích toàn phần của khối ru-bích là: 8,5 × 8,5 × 6 = 433,5 (cm²)

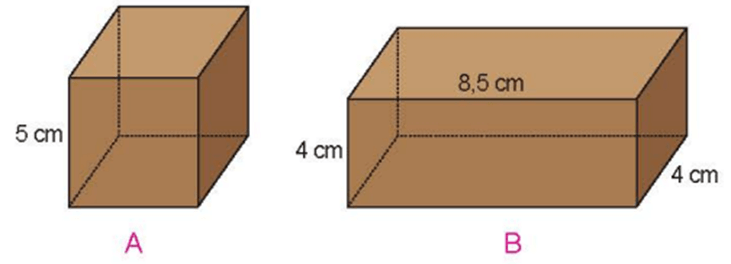
Giải Toán lớp 5 Tập 2 trang 116 Bài 3: Khối gỗ hình lập phương A và khối gỗ hình hộp chữ nhật B có kích thước như hình dưới đây.

a) Tính diện tích xung quanh của mỗi khối gỗ.

b) Diện tích toàn phần của khối gỗ nào lớn hơn và lớn hơn bao nhiêu xăng-ti-mét vuông?

Lời giải:

a) Diện tích xung quanh của khối gỗ A là: 5 × 5 × 4 = 100 (cm²)

Diện tích xung quanh của khối gỗ B là: (4 + 8,5) × 2 × 4 = 100 (cm²)

b) Diện tích toàn phần của khối gỗ A là: 5 × 5 × 6 = 150 (cm²)

Diện tích toàn phần của khối gỗ B là: 100 + 8,5 × 4 × 2 = 168 (cm²)

Vì 168 cm² > 150 cm² nên diện tích toàn phần của khối gỗ B lớn hơn.

Diện tích toàn phần của khối gỗ B lớn hơn khối gỗ A số xăng-ti-mét vuông là:

168 – 150 = 18 (cm²)

Giải Toán lớp 5 trang 117 Tập 2

Giải Toán lớp 5 Tập 2 trang 117 Bài 4: Người ta quét vôi xung quanh tường và trần một phòng họp cao 4 m chiều rộng 6 m, chiều dài 8 m. Hỏi diện tích cần quét vôi là bao nhiêu mét vuông, biết tất cả các cửa của phòng họp có diện tích là 6,5 m².

Lời giải:

Diện tích xung quanh phòng họp là:

(6 + 8) × 2 × 4 = 112 (m²)

Diện tích trần nhà là:

6 × 8 = 48 (m²)

Diện tích cần quét vôi là:

112 + 48 – 6,5 = 153,5 (m²)

Đáp số: 153,5 m².

Giải Toán lớp 5 Tập 2 trang 117 Bài 5: Số?

Rô-bốt xếp 27 khối gỗ lập phương nhỏ thành một khối lập phương lớn rồi sơn tất cả các mặt của khối lập phương lớn đó như hình vẽ.

a) Số khối lập phương nhỏ được sơn 3 mặt là khối.

b) Số khối lập phương nhỏ được sơn 2 mặt là khối.

Lời giải:

a) Số khối lập phương nhỏ được sơn 3 mặt là 8 khối.

b) Số khối lập phương nhỏ được sơn 2 mặt là 12 khối.

Toán lớp 5 trang 117, 118 Tập 2 Luyện tập

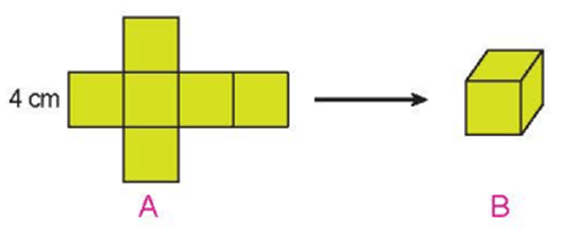
Giải Toán lớp 5 Tập 2 trang 117 Bài 1: Từ hình khai triển A gồm 6 hình vuông như hình dưới đây, Mai đã gấp được hình lập phương B. Tính diện tích xung quanh, diện tích toàn phần, thể tích của hình lập phương B.

Lời giải:

Diện tích xung quanh của hình lập phương B là: 4 × 4 × 4 = 64 (cm²)

Diện tích toàn phần của hình lập phương B là: 4 × 4 × 6 = 96 (cm²)

Thể tích của hình lập phương B là: 4 × 4 × 4 = 64 (cm³)

Giải Toán lớp 5 trang 118 Tập 2

Giải Toán lớp 5 Tập 2 trang 118 Bài 2: Trong một xưởng điêu khắc đá ở Ngũ Hành Sơn có khối đá dạng hình lập phương A cạnh 0,8 m và khối đá dạng hình hộp chữ nhật B có chiều cao 0,8 m, chiều dài 0,6 m, chiều rộng 0,4 m. Hỏi khối đá nào nặng hơn và nặng hơn bao nhiêu ki-lô-gam? Biết 1 m³ đá cân nặng 2,75 tấn.

Lời giải:

Thể tích khối đá A là:

0,8 × 0,8 × 0,8 = 0,512 (m³)

Thể tích khối đá B là:

0,8 × 0,6 × 0,4 = 0,192 (m³)

Thể tích khối đá A hơn thể tích khối đá B là:

0,512 – 0,192 = 0,32 (m³)

Khối đá A nặng hơn khối đá B là:

2,75 × 0,32 = 0,88 (tấn)

Đổi: 0,88 tấn = 880 kg

Đáp số: Khối đá A nặng hơn 880 kg.

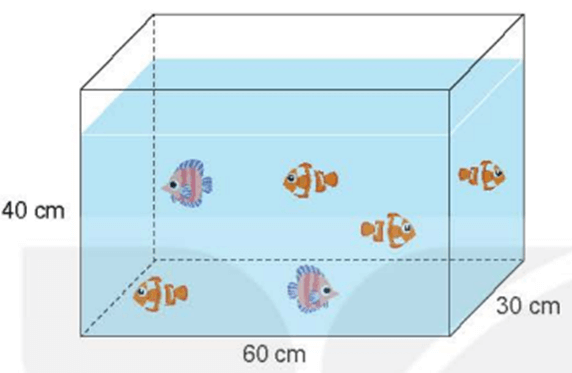
Giải Toán lớp 5 Tập 2 trang 118 Bài 3: Một bể cá có kích thước như hình dưới đây.

a) Tính thể tích bể cá.

b) Lúc đầu, mực nước trong bể bằng $\frac{3}{4}$ chiều cao của bể. Sau đó Nam cho vào bể một viên đá cảnh thì thấy mực nước lúc này cao 32,5 cm. Hỏi thể tích của viên đá cảnh đó là bao nhiêu xăng-ti-mét khối?

Lời giải:

a) Thể tích bể cá là:

60 × 30 × 40 = 72 000 (cm³)

b) Mực nước trong bể lúc đầu có chiều cao là:

40 × $\frac{3}{4}$ = 30 (cm)

Khi cho vào bể viên đá cảnh, mực nước dâng cao thêm là:

32,5 – 30 = 2,5 (cm)

Thể tích viên đá cảnh đó là:

60 × 30 × 2,5 = 4 500 (cm³)

Đáp số: a) 72 000 cm³

b) 4 500 cm³

Giải Toán lớp 5 Tập 2 trang 118 Bài 4: Số?

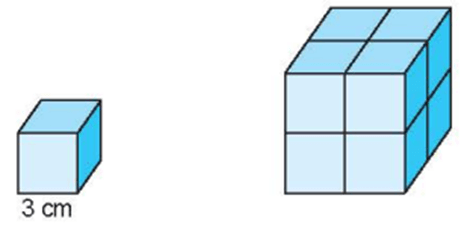
Một hình lập phương có cạnh 3 cm. Nếu tăng cạnh hình lập phương lên 2 lần thì:

a) Diện tích toàn phần hình lập phương tăng lên lần.

b) Thể tích hình lập phương tăng lên lần.

Lời giải:

a) Diện tích toàn phần hình lập phương tăng lên 4 lần.

b) Thể tích hình lập phương tăng lên 8 lần.

Giải thích:

a) Diện tích toàn phần của hình lập phương ban đầu là: 3 × 3 × 6 (cm²)

Diện tích toàn phần của hình lập phương sau khi cạnh tăng lên 2 lần là:

(3 × 2) × (3 × 2) × 6 = (3 × 3 × 6) × 4 (cm²)

Vậy diện tích toàn phần hình lập phương tăng lên 4 lần.

b) Thể tích của hình lập phương ban đầu là: 3 × 3 × 3 (cm³)

Thể tích của hình lập phương sau khi cạnh tăng lên 2 lần là:

(3 × 2) × (3 × 2) × (3 × 2) = (3 × 3 × 3) × 8 (cm³)

Vậy thể tích hình lập phương tăng lên 8 lần.