Bài 1 trang 111 Toán 7 Tập 2 Cánh diều
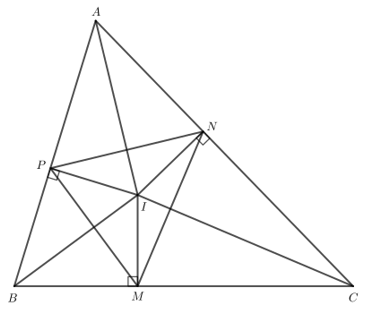
Tam giác ABC có ba đường phân giác cắt nhau tại I. Gọi M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB.
Giải Toán 7 Bài 11: Tính chất ba đường phân giác của tam giác - Cánh diều
Bài 1 trang 111 Toán lớp 7 Tập 2: Tam giác ABC có ba đường phân giác cắt nhau tại I. Gọi M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB.
a) Các tam giác IMN, INP, IPM có là tam giác cân không? Vì sao?
b) Các tam giác ANP, BPM, CMN có là tam giác cân không? Vì sao?
Lời giải:
a) Tam giác ABC có I là giao điểm ba đường phân giác nên I cách đều 3 cạnh của tam giác ABC.
Do đó IM = IN = IP.
Do IM = IN nên tam giác IMN cân tại I.
Do IN = IP nên tam giác INP cân tại I.
Do IP = IM nên tam giác IPM cân tại I.
b) Xét ∆AIP vuông tại P và ∆AIN vuông tại N có:
AI chung.
IP = IN (theo giả thiết).
Do đó ∆AIP = ∆AIN (cạnh huyền - cạnh góc vuông).
Suy ra AP = AN (2 cạnh tương ứng).
Tam giác ANP có AP = AN nên tam giác ANP cân tại A.
Xét ∆BIP vuông tại P và BIM vuông tại M có:
BI chung.
IP = IM (theo giả thiết).
Do đó ∆BIP = ∆BIM (cạnh huyền - cạnh góc vuông).
Suy ra BP = BM (2 cạnh tương ứng).
Tam giác BPM có BP = BM nên tam giác BPM cân tại B.
Xét ∆CIM vuông tại M và ∆CIN vuông tại N có:
CI chung.
IM = IN (theo giả thiết).
Do đó ∆CIM = ∆CIN (cạnh huyền - cạnh góc vuông).
Suy ra CM = CN (2 cạnh tương ứng).
Tam giác CMN có CM = CN nên tam giác CMN cân tại C.
Lời giải bài tập Toán 7 Bài 11: Tính chất ba đường phân giác của tam giác hay, chi tiết khác: