Luyện tập 3 trang 111 Toán 7 Tập 2 Cánh diều
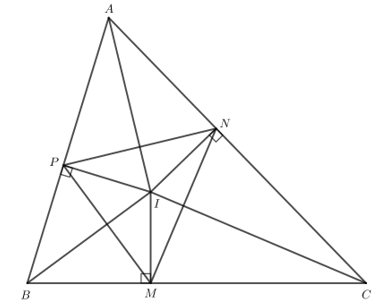
Cho tam giác ABC có I là giao điểm của ba đường phân giác. M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB. Chứng minh rằng: IA, IB, IC lần lượt là đường trung trực của các đoạn thẳng NP, PM, MN.
Giải Toán 7 Bài 11: Tính chất ba đường phân giác của tam giác - Cánh diều
Luyện tập 3 trang 111 Toán lớp 7 Tập 2: Cho tam giác ABC có I là giao điểm của ba đường phân giác. M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB. Chứng minh rằng: IA, IB, IC lần lượt là đường trung trực của các đoạn thẳng NP, PM, MN.
Lời giải:
+) Chứng minh IA là đường trung trực của NP.
Do IP = IN nên I thuộc đường trung trực của NP.
Xét ∆AIP vuông tại P và ∆AIN vuông tại N có:
AI chung.
IP = IN (theo giả thiết).
Do đó ∆AIP = ∆AIN (cạnh huyền - cạnh góc vuông).
Suy ra AP = AN (2 cạnh tương ứng).
Do AP = AN nên A thuộc đường trung trực của NP.
Do đó IA là đường trung trực của NP.
+) Chứng minh IB là đường trung trực của PM.
Do IP = IM nên I thuộc đường trung trực của PM.
Xét ∆BIP vuông tại P và ∆BIM vuông tại M có:
BI chung.
IP = IM (theo giả thiết).
Do đó ∆BIP = ∆BIM (cạnh huyền - cạnh góc vuông).
Suy ra BP = BM (2 cạnh tương ứng).
Do BP = BM nên B thuộc đường trung trực của PM.
Do đó IB là đường trung trực của PM.
+) Chứng minh IC là đường trung trực của MN.
Do IM = IN nên I thuộc đường trung trực của MN.
Xét ∆CIM vuông tại M và ∆CIN vuông tại N có:
CI chung.
IM = IN (theo giả thiết).
Do đó ∆CIM = ∆CIN (cạnh huyền - cạnh góc vuông).
Suy ra CM = CN (2 cạnh tương ứng).
Do CM = CN nên C thuộc đường trung trực của MN.
Do đó IC là đường trung trực của MN.
Lời giải bài tập Toán 7 Bài 11: Tính chất ba đường phân giác của tam giác hay, chi tiết khác: