Bài 4 trang 119 Toán 7 Tập 2 Cánh diều
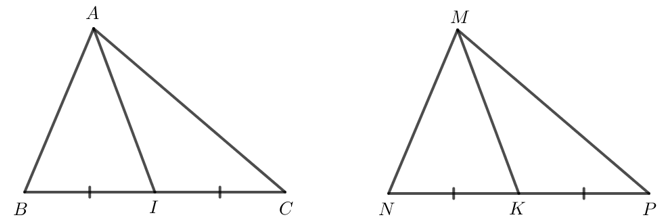
Cho hai tam giác ABC và MNP có: AB = MN, BC = NP, CA = PM. Gọi I và K lần lượt là trung điểm của BC và NP. Chứng minh: AI = MK.
Giải Toán 7 Bài tập cuối chương 7 - Cánh diều
Bài 4 trang 119 Toán lớp 7 Tập 2: Cho hai tam giác ABC và MNP có: AB = MN, BC = NP, CA = PM. Gọi I và K lần lượt là trung điểm của BC và NP. Chứng minh: AI = MK.
Lời giải:
Xét ∆ABC và ∆MNP có:
AB = MN (theo giả thiết).
BC = NP (theo giả thiết).
CA = PM (theo giả thiết).
Do đó ∆ABC = ∆MNP (c - c - c).
Suy ra .
Do I, K lần lượt là trung điểm của BC và NP mà BC = NP nên CI = PK.
Xét ∆ACI và ∆MPK có:
AC = MP (theo giả thiết).
(chứng minh trên).
CI = PK (chứng minh trên).
Do đó ∆ACI = ∆MPK (c - g - c).
Suy ra AI = MK (2 cạnh tương ứng).
Lời giải bài tập Toán 7 Bài tập cuối chương 7 trang 119, 120 hay, chi tiết khác:
Bài 1 trang 119 Toán lớp 7 Tập 2: Cho tam giác ABC có: . a) Tính . ....
Bài 2 trang 119 Toán lớp 7 Tập 2: Tìm các số đo x, y trong Hình 140 ....