X

Giải Toán lớp 7 Cánh diều

Mục lục Giải bài tập Toán 7 Giải bài tập Toán lớp 7 Tập 1 Giải bài tập Toán lớp 7 Tập 2 Chương 5: Một số yếu tố thống kê và xác suất Bài 1: Thu thập, phân loại và biểu diễn dữ liệu Bài 2: Phân tích và xử lí dữ liệu Bài 3: Biểu đồ đoạn thẳng Bài 4: Biểu đồ hình quạt tròn Bài 5: Biến cố trong một số trò chơi đơn giản Bài 6: Xác suất của biến cố ngẫu nhiên trong một số trò chơi đơn giản Bài tập cuối chương 5 Chủ đề 3: Dung tích phổi Chương 6: Biểu thức đại số Bài 1: Biểu thức số. Biểu thức đại số Bài 2: Đa thức một biến. Nghiệm của đa thức một biến Bài 3: Phép cộng, phép trừ đa thức một biến Bài 4: Phép nhân đa thức một biến Bài 5: Phép chia đa thức một biến Bài tập cuối chương 6 Chương 7: Tam giác Bài 1: Tổng các góc của một tam giác Bài 2: Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác Bài 3: Hai tam giác bằng nhau Bài 4: Trường hợp bằng nhau thứ nhất của tam giác: cạnh - cạnh - cạnh Bài 5: Trường hợp bằng nhau thứ hai của tam giác: cạnh - góc - cạnh Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc Bài 7: Tam giác cân Bài 8: Đường vuông góc và đường xiên Bài 9: Đường trung trực của một đoạn thẳng Bài 10: Tính chất ba đường trung tuyến của tam giác Bài 11: Tính chất ba đường phân giác của tam giác Bài 12: Tính chất ba đường trung trực của tam giác Bài 13: Tính chất ba đường cao của tam giác Bài tập cuối chương 7 Thực hành một số phần mềm

Bài 8 trang 120 Toán 7 Tập 2 Cánh diều

❮ Bài trước Bài sau ❯

Cho tam giác ABC có O là giao điểm của ba đường trung trực. Qua các điểm A, B, C lần lượt kẻ các đường thẳng vuông góc với OA, OB, OC, hai trong ba đường đó lần lượt cắt nhau tại M, N, P (Hình 144).

Giải Toán 7 Bài tập cuối chương 7 - Cánh diều

Bài 8 trang 120 Toán lớp 7 Tập 2: Cho tam giác ABC có O là giao điểm của ba đường trung trực. Qua các điểm A, B, C lần lượt kẻ các đường thẳng vuông góc với OA, OB, OC, hai trong ba đường đó lần lượt cắt nhau tại M, N, P (Hình 144).

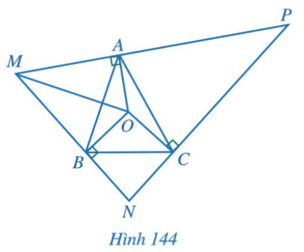
Bài 8 trang 120 Toán 7 Tập 2 Cánh diều

Chứng minh:

a) ∆OMA = ∆OMB và tia MO là tia phân giác của góc NMP;

b) O là giao điểm ba đường phân giác của tam giác MNP.

Lời giải:

a) Do O là giao điểm ba đường trung trực của tam giác ABC nên OA = OB = OC.

Xét ∆OMA vuông tại A và ∆OMB vuông tại B có:

OM chung.

OA = OB (chứng minh trên).

Do đó ∆OMA = ∆OMB (cạnh huyền - cạnh góc vuông).

Suy ra OMA^=OMB^ (2 góc tương ứng).

Do đó MO là tia phân giác của BMA^ hay MO là tia phân giác của NMP^.

b) Thực hiện nối OP.

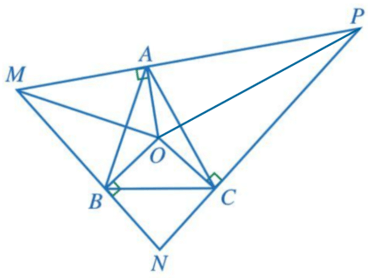
Bài 8 trang 120 Toán 7 Tập 2 Cánh diều

Xét ∆OPA vuông tại A và ∆OPC vuông tại C có:

OP chung.

OA = OC (chứng minh trên).

Do đó ∆OPA = ∆OPC (cạnh huyền - cạnh góc vuông).

Suy ra OPA^=OPC^ (2 góc tương ứng).

Do đó PO là tia phân giác của CPA^ hay PO là tia phân giác của NPM^.

Trong tam giác NMP có O là giao điểm hai đường phân giác của góc M và góc P.

Mà ba đường phân giác của tam giác cùng đi qua một điểm nên O là giao điểm ba đường phân giác của tam giác MNP.

Lời giải bài tập Toán 7 Bài tập cuối chương 7 trang 119, 120 hay, chi tiết khác:

Xem thêm lời giải bài tập Toán lớp 7 Cánh diều hay, chi tiết khác:

❮ Bài trước Bài sau ❯
2018 © All Rights Reserved. DMCA.com Protection Status