Bài 6 trang 119 Toán 7 Tập 2 Cánh diều

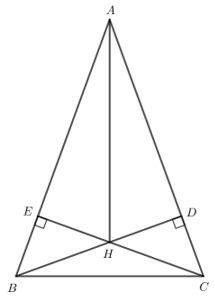
Cho tam giác ABC cân tại A có . Hai đường cao BD và CE cắt nhau tại H.

Giải Toán 7 Bài tập cuối chương 7 - Cánh diều

Bài 6 trang 119 Toán lớp 7 Tập 2: Cho tam giác ABC cân tại A có $\hat{A B C} = 70 °$ . Hai đường cao BD và CE cắt nhau tại H.

a) Tính số đo các góc còn lại của tam giác ABC.

b) Chứng minh BD = CE.

c) Chứng minh tia AH là tia phân giác của góc BAC.

Lời giải:

Bài 6 trang 119 Toán 7 Tập 2 Cánh diều

a) Tam giác ABC cân tại A nên AB = AC và $\hat{A B C} = \hat{A C B} = 70 °$ .

Trong tam giác ABC: $\hat{B A C} = 180 ° - \hat{A B C} - \hat{A C B}$ = 180° - 70° - 70° = 40°.

b) Xét ∆ADB vuông tại D và ∆AEC vuông tại E có:

AB = AC (chứng minh trên).

$\hat{A}$ chung.

Do đó ∆ADB = ∆AEC (cạnh huyền - góc nhọn).

Suy ra BD = CE (2 cạnh tương ứng).

c) Do ∆ADB = ∆AEC (cạnh huyền - góc nhọn) nên AD = AE (2 cạnh tương ứng).

Xét ∆AEH vuông tại E và ∆ADH vuông tại D có:

AE = AD (chứng minh trên).

AH chung.

Do đó ∆AEH = ∆ADH (cạnh huyền - cạnh góc vuông).

Suy ra $\hat{H A E} = \hat{H A D}$ (2 góc tương ứng).

Do đó AH là tia phân giác của $\hat{B A C}$ .

Lời giải bài tập Toán 7 Bài tập cuối chương 7 trang 119, 120 hay, chi tiết khác: