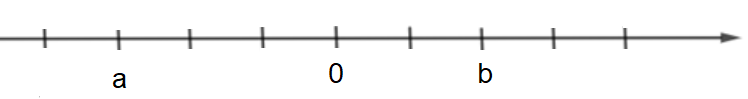Giải Toán 7 trang 9 Tập 1 Cánh diều

---

Haylamdo biên soạn và sưu tầm giải Toán 7 trang 9 Tập 1 trong Bài 1. Tập hợp Q các số hữu tỉ Toán 7 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 9.

Giải Toán 7 trang 9 Tập 1 Cánh diều

Hoạt động 4 trang 9 Toán lớp 7 Tập 1: So sánh:

a) $-\frac{1}{3}$ và $\frac{-2}{5}$;

b) 0,125 và 0,13;

c) – 0,6 và $\frac{-2}{3}$.

Lời giải:

a) Ta có $-\frac{1}{3}=\frac{-1}{3}$.

Các số $\frac{-1}{3}$ và $\frac{-2}{5}$ là các phân số có mẫu số dương. 

Thực hiện quy đồng mẫu các phân số, ta được:

 $\frac{-1}{3}=\frac{(-1).5}{3.5}=\frac{-5}{15}$; $\frac{-2}{5}=\frac{(-2).3}{5.3}=\frac{-6}{15}$ .

Vì − 5 > − 6 nên $\frac{-5}{15}>\frac{-6}{15}$ hay $\frac{-1}{3}>\frac{-2}{5}$.

Vậy $-\frac{1}{3}>\frac{-2}{5}$.

b) Cách 1: Hai số 0,125 và 0,13 đều có phần số nguyên là 0.

Ta so sánh chữ số phần thập phân của hai số:

- Chữ số hàng phần mười của hai số đều là 1.

- Chữ số hàng phần trăm của số 0,125 là 2 và của số 0,13 là 3. 

Vì 2 < 3 nên 0,125 < 0,13.

Vậy 0,125 < 0,13.

Cách 2: Viết các số 0,125 và 0,13 dưới dạng các phân số có mẫu số dương rồi rút gọn, ta được:

 $\mathrm{0,125}=\frac{125}{1000}=\frac{1}{8}$; $\mathrm{0,13}=\frac{13}{100}$.

Ta thực hiện quy đồng mẫu các phân số đó như sau:

$\frac{1}{8}=\frac{1.25}{8.25}=\frac{25}{200}$; $\frac{13}{100}=\frac{13.2}{100.2}=\frac{26}{200}$.

Vì 25 < 26 nên $\frac{25}{100}<\frac{26}{100}$ hay $\frac{1}{8}<\frac{13}{100}$.

Vậy 0,125 < 0,13.

c) – 0,6 và $\frac{-2}{3}$.

Ta có $-\mathrm{0,6}=\frac{-6}{10}=\frac{-3}{5}$.

Thực hiện quy đồng mẫu số hai phân số, ta được:

 $\frac{-3}{5}=\frac{(-3).3}{5.3}=\frac{-9}{15}$; $\frac{-2}{3}=\frac{(-2).5}{3.5}=\frac{-10}{15}$.

Vì – 9 > – 10 nên $\frac{-9}{15}>\frac{-10}{15}$ hay $-\mathrm{0,6}>\frac{-2}{3}$.

Vậy $-\mathrm{0,6}>\frac{-2}{3}$.

Luyện tập 4 trang 9 Toán lớp 7 Tập 1: So sánh:

a) – 3,23 và – 3,32;

b) $\frac{-7}{3}$ và – 1,25.

Lời giải:

a) Cách 1: Số đối của – 3,23 và – 3,32 lần lượt là 3,23 và 3,32.

Hai số 3,23 và 3,32 đều có phần nguyên là 3.

Ta so sánh phần thập phân: Chữ số hàng phần mười của số 3,23 và 3,32 lần lượt là 2 và 3.

Vì 2 < 3 nên 3,23 < 3,32 do đó – 3,23 > – 3,32.

Vậy – 3,23 > – 3,32.

Cách 2: Viết các số – 3,23 và – 3,32 dưới dạng các phân số có mẫu số dương rồi rút gọn, ta được:

 $-\mathrm{3,23}=\frac{-323}{100}$; $-\mathrm{3,32}=\frac{-332}{100}$.

Vì – 323 > – 332 nên $\frac{-323}{100}>\frac{-332}{100}$ hay – 3,23 > – 3,32.

Vậy – 3,23 > – 3,32.

b) Ta có: $-1,25=\frac{-125}{100}=\frac{\left(-125\right):25}{100:25}=\frac{-5}{4}; -\frac{7}{3}=\frac{-7}{3}$

Ta đi quy đồng mẫu số hai phân số trên:

$\frac{-5}{4}=\frac{\left(-5\right).3}{4.3}=\frac{-15}{12};\frac{-7}{3}=\frac{\left(-7\right).4}{3.4}=\frac{-28}{12}$

Vì –15 > –28 nên $\frac{-15}{12}>\frac{-28}{12}$

Do đó, $\frac{-5}{4}>\frac{-7}{3}$ hay $-1,25 >-\frac{7}{3}$

Vậy $-1,25 >-\frac{7}{3}$.

Hoạt động 5 trang 9, 10 Toán lớp 7 Tập 1: Giả sử hai điểm a, b lần lượt biểu diễn hai số nguyên a, b trên trục số nằm ngang. Với a < b, nêu nhận xét về vị trí của điểm a so với điểm b trên trục số đó.

Lời giải:

Hai điểm a, b lần lượt biểu diễn hai số nguyên a, b trên trục số nằm ngang.

Xét a < b.

+) Với a < 0, b < 0 và a < b.

Ta có hình vẽ minh họa như sau:

 

Khi đó, điểm a nằm bên trái điểm b.

+) Với a < 0, b > 0 và a < b.

Ta có hình vẽ minh họa như sau:

Khi đó, điểm a nằm bên trái điểm b.

+) Với a > 0, b > 0 và a < b.

Ta có hình vẽ minh họa như sau:

Khi đó, điểm a nằm bên trái điểm b.

Vậy với a < b thì điểm a nằm bên trái điểm b.

Lời giải bài tập Toán lớp 7 Bài 1. Tập hợp Q các số hữu tỉ Cánh diều hay khác:

• Giải Toán 7 trang 5 Tập 1
• Giải Toán 7 trang 6 Tập 1
• Giải Toán 7 trang 7 Tập 1
• Giải Toán 7 trang 8 Tập 1
• Giải Toán 7 trang 10, 11 Tập 1