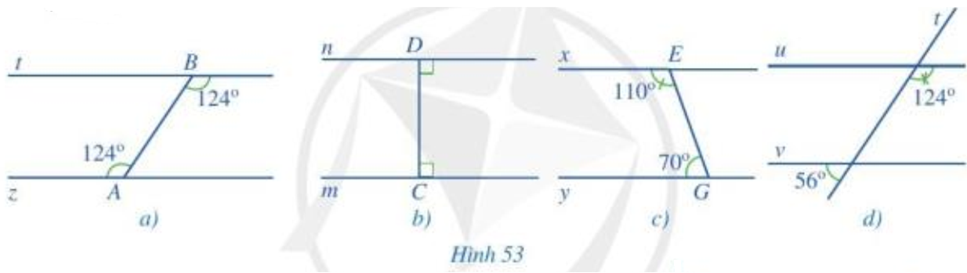
Tìm cặp đường thẳng song song trong mỗi hình 53a, 53b, 53c, 53d và giải thích vì sao.
Câu hỏi:
Tìm cặp đường thẳng song song trong mỗi hình 53a, 53b, 53c, 53d và giải thích vì sao.
Trả lời:
- Hình 53a:
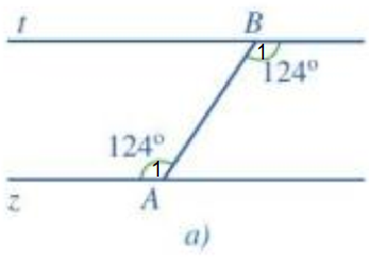
Ta có: .
Mà và ở vị trí so le trong.
Do đó t // z.
- Hình 53b:
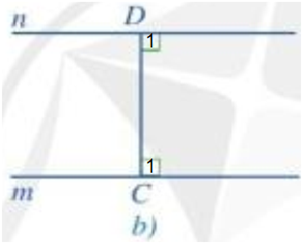
Ta có: nên .
Mà và là hai góc trong cùng phía.
Do đó m // n.
- Hình 53c:
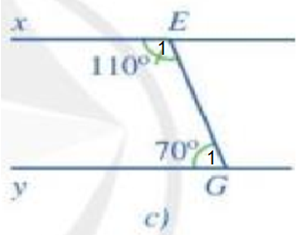
Ta có: nên .
Mà và là hai góc trong cùng phía.
Do đó x // y.
- Hình 53d: Gọi giao điểm của hai đường thẳng u và v với đường thẳng t lần lượt tại hai điểm M và N.
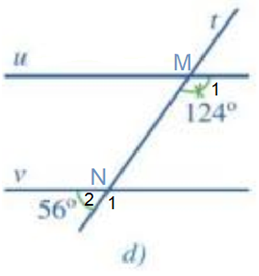
Vì và là hai góc kề bù nên .
Khi đó, .
Ta có: .
Mà và là hai góc đồng vị.
Do đó u // v.