Bài 3 trang 75 Toán 7 Tập 1 Chân trời sáng tạo
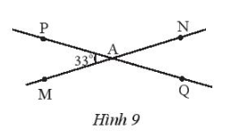
Cho hai đường thẳng MN, PQ cắt nhau tại A và tạo thành (Hình 9).
Giải Toán 7 Bài 2: Tia phân giác - Chân trời sáng tạo
Bài 3 trang 75 Toán 7 Tập 1: Cho hai đường thẳng MN, PQ cắt nhau tại A và tạo thành ^PAM=33o (Hình 9).
a) Tính số đo các góc còn lại.
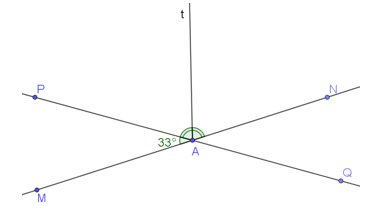
b) Vẽ At là tia phân giác của ^PAN. Hãy tính số đo của ^tAQ. Vẽ tia At’ là tia đối của tia At. Giải thích tại sao At’ là tia phân giác của ^MAQ.
Lời giải:
Thiếu số thứ tự ý a
a) Vì ^PAM và ^PAN là hai góc kề bù nên:
^PAM+^PAN=180o
33o+^PAN=180o
Suy ra ^PAN=180o−33o=147o.
Mặt khác, ^NAQ=^PAM=33o (hai góc đối đỉnh)
^MAQ=^PAN=147o (hai góc đối đỉnh).
Vậy số đo các góc còn lại là: ^PAN=147o; ^NAQ=33o; ^MAQ=147o.
b) Vẽ tia At là tia phân giác của ^PAN (như hình vẽ):
Vì tia At là tia phân giác của ^PAN nên:
^tAP=^tAN=^PAN2
=147o2=73,5o.
Ta có:
^tAQ=^tAN+^NAQ
=73,5o+33o=106,5o.
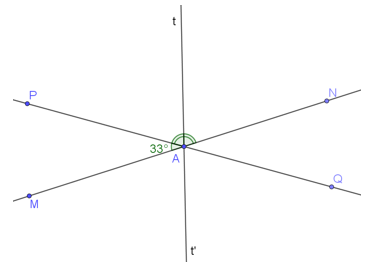
Tia At’ là tia đối của tia At (như hình vẽ).
Tia At’ nằm giữa hai tia AM và AQ (1)
Ta có: ^tAP=t' (hai góc đối đỉnh);
(hai góc đối đỉnh).
Mà (vì tia At là tia phân giác của ).
Suy ra (2)
Từ (1) và (2) suy ra: At’ là tia phân giác của .
Lời giải bài tập Toán 7 Bài 2: Tia phân giác hay, chi tiết khác:
Thực hành 1 trang 73 Toán 7 Tập 1: Tìm tia phân giác của các góc: và ....
Vận dụng 1 trang 74 Toán 7 Tập 1: Em hãy cho biết khi cân thăng bằng thì kim ở vị trí nào của ....
