Bài 2 trang 108 Toán 8 Tập 1 Cánh diều
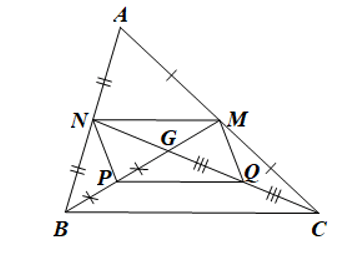
Cho tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G. Gọi P và Q lần lượt là trung điểm của GB và GC. Chứng minh tứ giác PQMN là hình bình hành.
Giải Toán 8 Bài 4: Hình bình hành - Cánh diều
Bài 2 trang 108 Toán 8 Tập 1: Cho tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại G. Gọi P và Q lần lượt là trung điểm của GB và GC. Chứng minh tứ giác PQMN là hình bình hành.
Lời giải:
• Xét ΔABC có hai đường trung tuyến BM và CN cắt nhau tại G (giả thiết) nên G là trọng tâm của ΔABC.
Suy ra ; (tính chất trọng tâm của tam giác) (1)
Mà P là trung điểm của GB (giả thiết) nên (2)
Q là trung điểm của GC (giả thiết) nên (3)
Từ (1), (2) và (3) suy ra GM = GP và GN = GQ.
• Xét tứ giác PQMN có: GM = GP và GN = GQ (chứng minh trên)
Do đó tứ giác PQMN có hai đường chéo MP và NQ cắt nhau tại trung điểm G của mỗi đường nên là hình bình hành.
Lời giải bài tập Toán 8 Bài 4: Hình bình hành hay, chi tiết khác:
Luyện tập 1 trang 106 Toán 8 Tập 1: Cho hình bình hành ABCD có , AB = 4 cm, BC = 5 cm ....
Hoạt động 3 trang 106, 107 Toán 8 Tập 1: a) Cho tứ giác ABCD có AB = CD, BC = DA (Hình 39) ....