Hoạt động 3 trang 106, 107 Toán 8 Tập 1 Cánh diều

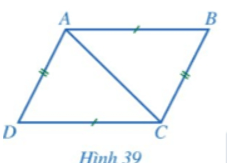
a) Cho tứ giác ABCD có AB = CD, BC = DA (Hình 39).

Giải Toán 8 Bài 4: Hình bình hành - Cánh diều

Hoạt động 3 trang 106, 107 Toán 8 Tập 1: a) Cho tứ giác ABCD có AB = CD, BC = DA (Hình 39).

• Hai tam giác ABC và CDA có bằng nhau hay không? Từ đó, hãy so sánh các cặp góc: $\hat{B A C}$ và $\hat{D C A}$ ; $\hat{A C B}$ và $\hat{C A D}$ .

• ABCD có phải là hình bình hành hay không?

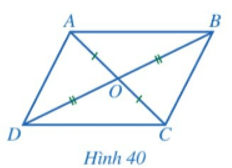
Hoạt động 3 trang 106, 107 Toán 8 Tập 1 Cánh diều | Giải Toán 8

b) Cho tứ giác ABCD có hai đường chéo AC và BD cắt nhau tại trung điểm O của mỗi đường (Hình 40).

• Hai tam giác ABO và CDO có bằng nhau hay không? Từ đó, hãy so sánh các cặp góc: $\hat{B A C}$ và $\hat{D C A}$ ; $\hat{A C B}$ và $\hat{C A D}$ .

• ABCD có phải là hình bình hành hay không?

Hoạt động 3 trang 106, 107 Toán 8 Tập 1 Cánh diều | Giải Toán 8

Lời giải:

a) • Xét ΔABC và ΔCDA có:

AB = CD (giả thiết); BC = DA (giả thiết); AC là cạnh chung

Do đó ΔABC = ΔCDA (c.c.c)

Suy ra $\hat{B A C} = \hat{D C A}$ và $\hat{A C B} = \hat{C A D}$ (các cặp góc tương ứng).

• Ta có $\hat{B A C} = \hat{D C A}$ và $\hat{B A C}, \hat{D C A}$ ở vị trí so le trong nên AB // CD.

$\hat{A C B} = \hat{C A D}$ và $\hat{A C B}, \hat{C A D}$ ở vị trí so le trong nên AD // BC.

Tứ giác ABCD có AB // CD và AD // BC nên là hình bình hành.

b) • Xét ΔABO và ΔCDO có:

OA = OC (giả thiết); $\hat{A O B} = \hat{C O D}$ (đối đỉnh); OB = OD (giả thiết)

Do đó ΔABO = ΔCDO (c.g.c)

Suy ra $\hat{B A O} = \hat{D C O}$ (cặp góc tương ứng)

Hay $\hat{B A C} = \hat{D C A}$ .

Chứng minh tương tự ta cũng có: ΔCBO = ΔADO (c.g.c)

Suy ra $\hat{O C B} = \hat{O A D}$ (cặp góc tương ứng)

Hay $\hat{A C B} = \hat{C A D}$ .

• Ta có $\hat{B A C} = \hat{D C A}$ và $\hat{B A C}, \hat{D C A}$ ở vị trí so le trong nên AB // CD.

$\hat{A C B} = \hat{C A D}$ và $\hat{A C B}, \hat{C A D}$ ở vị trí so le trong nên AD // BC.

Tứ giác ABCD có AB // CD và AD // BC nên là hình bình hành.

Lời giải bài tập Toán 8 Bài 4: Hình bình hành hay, chi tiết khác: