Vận dụng 4 trang 71 Toán 8 Tập 1 Chân trời sáng tạo

---

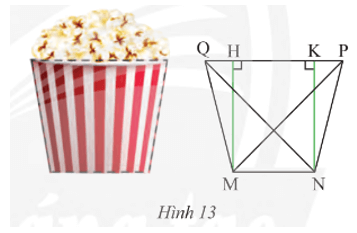
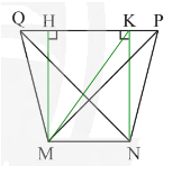
Mặt cắt của một li giấy đựng bỏng ngô có dạng hình thang cân MNPQ (Hình 13) với hai đáy MN = 6 cm, PQ = 10 cm và độ dài hai đường chéo MP = NQ = cm. Tính độ dài đường cao và cạnh bên của hình thang.

Giải Toán 8 Bài 3: Hình thang – Hình thang cân - Chân trời sáng tạo

Vận dụng 4 trang 71 Toán 8 Tập 1: Mặt cắt của một li giấy đựng bỏng ngô có dạng hình thang cân MNPQ (Hình 13) với hai đáy MN = 6 cm, PQ = 10 cm và độ dài hai đường chéo MP = NQ = $8\sqrt{2}$ cm. Tính độ dài đường cao và cạnh bên của hình thang.

Lời giải:

• MNPQ là hình thang cân nên MN // QP; MQ = NP; $\widehat{MQP}=\widehat{NPQ}$ (tính chất hình thang cân).

• Ta có: MN // QP (chứng minh trên) và NK ⊥ QP (giả thiết)

Suy ra NK ⊥ MN hay $\widehat{MNK}=90°$.

Xét DMHK và DKNM có:

$\widehat{MHK}=\widehat{KNM}=90°$;

MK là cạnh huyền chung;

$\widehat{MKH}=\widehat{KMN}$ (hai góc so le trong của QP // MN).

Do đó DMHK = DKNM (cạnh huyền – góc nhọn)

Suy ra HK = NM = 6 cm (hai cạnh tương ứng).

• Xét DMHQ và DNKP có:

$\widehat{MHQ}=\widehat{NKP}=90°$;

MQ = NP (chứng minh trên);

$\widehat{MQH}=\widehat{NPK}$ (chứng minh trên).

Do đó DMHQ = DNKP (cạnh huyền – góc nhọn).

Suy ra QH = PK (hai cạnh tương ứng).

Mà QH + HK + PK = QP

Hay 2QH = QP – HK

Khi đó QH = PK = $\frac{QP-HK}{2}=\frac{10-6}{2}=2\left(cm\right)$ 

Nên HP = HK + KP = 6 + 2 = 8 (cm).

• Áp dụng định lí Pythagore vào DMHP vuông tại H, ta có:

MP² = MH² + HP²

Suy ra MH² = MP² – HP² = ${\left(8\sqrt{2}\right)}^2-8^2=128-64=64=8^2$

Do đó MH = 8 cm.

Áp dụng định lí Pythagore vào DMHQ vuông tại H, ta có:

MQ² = MH² + HQ² = 8² + 2² = 64 + 4 = 68

Suy ra $MQ=2\sqrt{17}$ (cm).

Vậy hình thang cân MNPQ có độ dài đường cao là MH = NK = 8 cm; độ dài cạnh bên là MQ = NP = $2\sqrt{17}$ cm.

Lời giải bài tập Toán 8 Bài 3: Hình thang – Hình thang cân hay, chi tiết khác:

• Khởi động trang 68 Toán 8 Tập 1: Mái ngói của trụ sở Ủy ban nhân dân Thành phố Hồ Chí Minh có hình dạng một tứ giác ABCD. Nêu nhận xét của em về hai cạnh AB và CD của tứ giác này ....

• Khám phá 1 trang 68 Toán 8 Tập 1: Tứ giác ABCD (Hình 1b) là hình vẽ minh hoạ một phần của chiếc thang ở Hình la. Nêu nhận xét của em về hai cạnh AB và CD của tứ giác này? ....

• Thực hành 1 trang 69 Toán 8 Tập 1: Tìm các góc chưa biết của hình thang MNPQ có hai đáy là MN và QP trong mỗi trường hợp sau và nêu nhận xét của em ....

• Vận dụng 1 trang 69 Toán 8 Tập 1: Một mặt tường của chân tháp cột cờ Hà Nội có dạng hình thang cân ABCD (Hình 4). ....

• Vận dụng 2 trang 69 Toán 8 Tập 1: Tứ giác EFGH có các góc cho như trong Hình 5. a) Chứng minh rằng EFGH là hình thang ....

• Khám phá 2 trang 69 Toán 8 Tập 1: a) Cho hình thang cân ABCD có hai đáy là AB và CD (AB > CD). Qua C vẽ đường thẳng song song với AD và cắt AB tại E (Hình 6a) ....

• Thực hành 2 trang 70 Toán 8 Tập 1: Tìm các đoạn thẳng bằng nhau trong hình thang cân MNPQ có hai đáy là MN và PQ ....

• Vận dụng 3 trang 70 Toán 8 Tập 1: Một khung cửa sổ hình thang cân có chiều cao 3 m, hai đáy là 3 m và 1 m (Hình 9). Tìm độ dài hai cạnh bên và hai đường chéo ....

• Khám phá 3 trang 70 Toán 8 Tập 1: Cho hình thang ABCD có hai đáy là AB, CD và có hai đường chéo bằng nhau (Hình 10). Vẽ đường thẳng đi qua C, song song với BD và cắt AB tại E ....

• Thực hành 3 trang 71 Toán 8 Tập 1: Sử dụng thước đo góc và thước đo độ dài để tìm hình thang cân trong các tứ giác ở Hình 12 ....

• Bài 1 trang 71 Toán 8 Tập 1: Tìm x và y ở các hình sau ....

• Bài 2 trang 71 Toán 8 Tập 1: Cho tứ giác ABCD có AB = AD, BD là tia phân giác của góc B. Chứng minh rằng ABCD là hình thang ....

• Bài 3 trang 72 Toán 8 Tập 1: Cho tam giác nhọn ABC có AH là đường cao. Tia phân giác của góc B cắt AC tại M. Từ M kẻ đường thẳng vuông góc với AH và cắt AB tại N ....

• Bài 4 trang 72 Toán 8 Tập 1: Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác của góc B cắt AC tại D. Trên BC lấy điểm E sao cho BE = BA ....

• Bài 5 trang 72 Toán 8 Tập 1: Tứ giác nào trong Hình 15 là hình thang cân? ....

• Bài 6 trang 72 Toán 8 Tập 1: Cho hình thang cân ABCD có AB // CD. Qua giao điểm E của AC và BD, ta vẽ đường thẳng song song với AB và cắt AD ....

• Bài 7 trang 72 Toán 8 Tập 1: Mặt bên của một chiếc va li (Hình 17a) có dạng hình thang cân và được vẽ lại như Hình 17b. Biết hình thang đó có độ dài đường cao là 60 cm ....