b) Bao nhiêu hạng tử bậc nhất? Cho ví dụ

Đơn thức −2³x²yz³ có

A. hệ số −2, bậc 8.

B. hệ số −2³, bậc 5.

C. hệ số −1, bậc 9.

D. hệ số −2³, bậc 6.

Gọi T là tổng, H là hiệu của hai đa thức 3x²y – 2xy² + xy và –2x²y + 3xy² + 1. Khi đó:

A. T = x²y – xy² + xy + 1 và H = 5x²y – 5xy² + xy – 1.

B. T = x²y + xy² + xy + 1 và H = 5x²y – 5xy² + xy – 1.

C. T = x²y + xy² + xy + 1 và H = 5x²y – 5xy² – xy – 1.

D. T = x²y + xy² + xy – 1 và H = 5x²y + 5xy² + xy – 1.

Tích của hai đơn thức 6x²yz và −2y²z² là đơn thức

A. 4x²y³z³.

B. −12x²y³z³.

C. −12x³y³z³.

D. 4x³y³z³.

Khi chia đa thức 8x³y² – 6x²y³ cho đơn thức −2xy, ta được kết quả là

A. −4x²y + 3xy².

B. −4xy² + 3x²y.

C. −10x²y + 4xy².

D. −10x²y + 4xy².

Cho biểu thức 3x³(x⁵ – y⁵) + y⁵(3x³ – y³).

a) Rút gọn biểu thức đã cho.

b) Tính giá trị của biểu thức đã cho nếu biết $y^4=x^4\sqrt{3}$.

Rút gọn biểu thức: $\frac{1}{4}\left(2x^2+y\right)\left(x^2-2y^2\right)+\frac{1}{4}\left(2x^2-y\right)\left(x^2+2y^2\right)$.

Bạn Thành dùng một miếng bìa hình chữ nhật để làm một chiếc hộp (không nắp) bằng cách cắt bốn hình vuông cạnh x centimét ở bốn góc (H.1.3) rồi gấp lại. Biết rằng miếng bìa có chiều dài là y centimét, chiều rộng là z centimét.

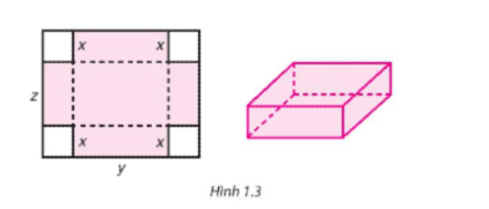
Tìm đa thức (ba biến x, y, z) biểu thị thể tích của chiếc hộp. Xác định bậc của đa thức đó.