Bạn Thành dùng một miếng bìa hình chữ nhật để làm một chiếc hộp (không nắp) bằng cách
Câu hỏi:
Bạn Thành dùng một miếng bìa hình chữ nhật để làm một chiếc hộp (không nắp) bằng cách cắt bốn hình vuông cạnh x centimét ở bốn góc (H.1.3) rồi gấp lại. Biết rằng miếng bìa có chiều dài là y centimét, chiều rộng là z centimét.
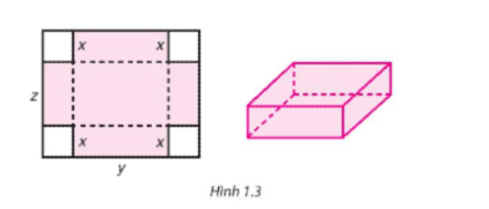
Tìm đa thức (ba biến x, y, z) biểu thị thể tích của chiếc hộp. Xác định bậc của đa thức đó.
Trả lời:
Cắt miếng bìa hình chữ nhật để làm một chiếc hộp (không nắp) thì chiếc hộp có:
• Chiều dài của đáy chiếc hộp là: y – 2x (cm)
• Chiều rộng của đáy chiếc hộp là: z – 2x (cm)
• Chiều rộng của chiếc hộp là x (cm)
Đa thức biểu thị thể tích của chiếc hộp là:
x(y – 2x)(z – 2x) = (xy – 2x2)(z – 2x) = xyz – 2x2y – 2x2z + 4x3.
Đa thức xyz – 2x2y – 2x2z + 4x3 có bậc là 3.
