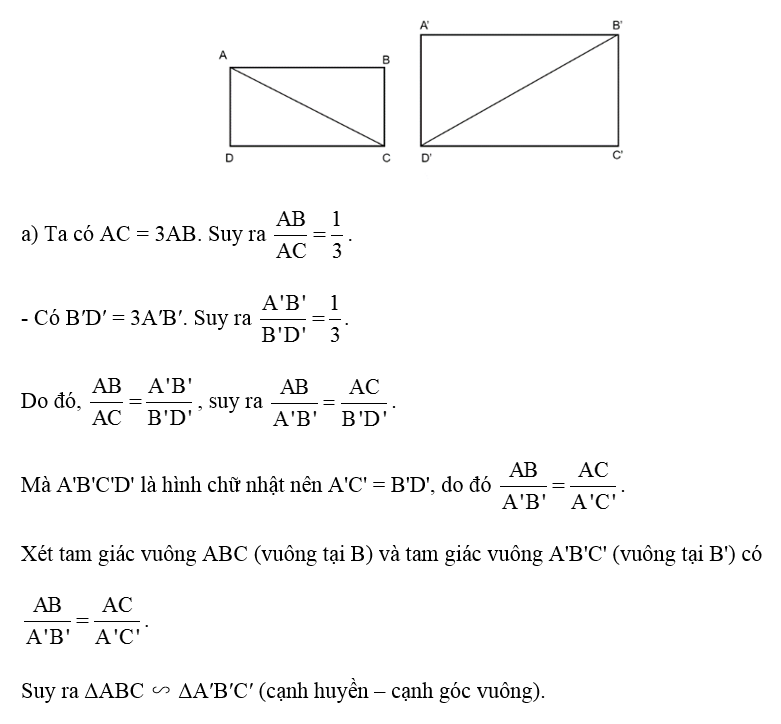
Cho hai hình chữ nhật ABCD và A'B'C'D' thỏa mãn AC = 3AB, B′D′ = 3A′B′.
Câu hỏi:
Cho hai hình chữ nhật ABCD và A'B'C'D' thỏa mãn AC = 3AB, B′D′ = 3A′B′.
a) Chứng minh rằng ΔABC ∽ ΔA'B'C'.
b) Nếu A'B' = 2AB và diện tích hình chữ nhật ABCD là 2 m2 thì diện tích hình chữ nhật A'B'C'D' là bao nhiêu?
Trả lời: