Cho hình bình hành ABCD. Các tia phân giác của góc A, B, C, D cắt nhau như trên Hình
Câu hỏi:
Cho hình bình hành ABCD. Các tia phân giác của góc A, B, C, D cắt nhau như trên Hình 3.58. Chứng minh rằng EFGH là hình chữ nhật.

Trả lời:
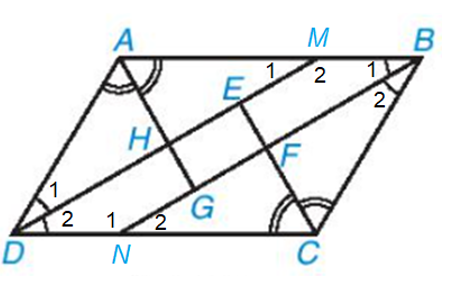
Vì tứ giác ABCD là hình bình hành nên AB // CD hay AM // DN.
Suy ra (hai góc so le trong)
Mà (vì DM là tia phân giác ).
Do đó nên tam giác ADM cân tại A.
Chứng minh tương tự, ta có tam giác BCN cân tại C.
Vì (vì DM, BN lần lượt là tia phân giác của ).
Mà (vì tứ giác ABCD là hình bình hành).
Do đó .
Tam giác ADM cân tại A, tam giác BCN cân tại C.
Mà nên suy ra .
Tứ giác BMDN có nên tứ giác BMDN là hình bình hành.
Suy ra DM // BN hay HE // GF.
Tam giác ADM cân tại A có AH là đường phân giác nên AH cũng là đường cao.
Suy ra nên .
Mà HE // GF suy ra (hai góc đồng vị).
Tương tự, ta cũng chứng minh được: .
Tứ giác EFGH có .
Do đó tứ giác EFGH là hình chữ nhật.
