Câu hỏi:
Cho tam giác ABC; M và N lần lượt là trung điểm của hai cạnh AB và AC. Lấy điểm P sao cho N là trung điểm của đoạn thẳng MP.
a) Hỏi tứ giác AMCP là hình gì? Vì sao?
Trả lời:
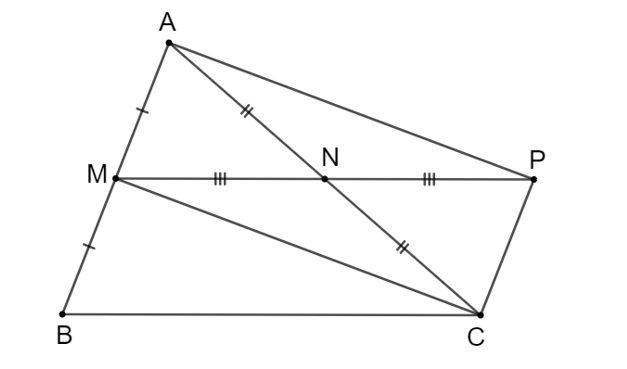
a) Tứ giác AMCP có hai đường chéo AC và MP cắt nhau tại trung điểm N của mỗi đường.
Do đó tứ giác AMCP là hình bình hành.
Câu 1:
b) Với điều kiện nào của tam giác ABC thì tứ giác AMCP là hình chữ nhật; hình thoi; hình vuông?
Câu 2:
Cho hình bình hành ABCD. Các tia phân giác của góc A, B, C, D cắt nhau như trên Hình 3.58. Chứng minh rằng EFGH là hình chữ nhật.
Câu 3:
Một khung tre hình chữ nhật có lắp đinh vít tại bốn đỉnh. Khi khung tre này bị xô lệch (do các đinh vít bị lỏng), các góc không còn vuông nữa thì khung đó là hình gì? Tại sao? Hỏi khi nẹp thêm một đường chéo vào khung đó thì nó còn bị xô lệch không?
Câu 4:
Gọi Ou và Ov lần lượt là hai tia phân giác của hai góc kề bù xOy và x’Oy; A là một điểm khác O trên tia Ox. Gọi B và C là chân đường vuông góc hạ từ A lần lượt xuống đường thẳng chứa Ou và Ov. Hỏi tứ giác OBAC là hình gì? Vì sao?
