Cho hình bình hành ABCD (H.3.30). a) Chứng minh tam giác ABC = tam giác CDA.
Câu hỏi:
Cho hình bình hành ABCD (H.3.30).
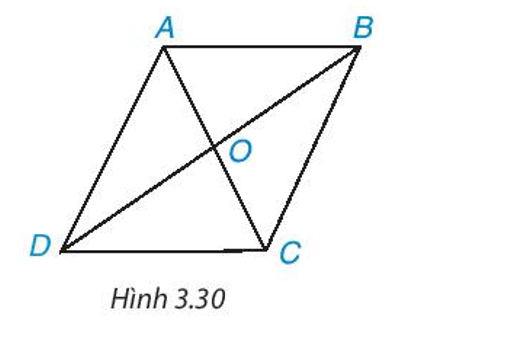
a) Chứng minh ∆ABC = ∆CDA.
Từ đó suy ra AB = CD, AD = BC và .
Trả lời:
a) Vì ABCD là hình bình hành nên AB // CD; AD // BC.
Suy ra (hai góc so le trong).
Xét ∆ABC và ∆CDA có:
(chứng minh trên);
Cạnh AC chung.
(chứng minh trên);
Do đó ∆ABC = ∆CDA (g.c.g).
Suy ra AB = CD, AD = BC (các cặp cạnh tương ứng); (hai góc tương ứng).