Vẽ hình bình hành, biết hai cạnh liên tiếp bằng 3 cm, 4 cm và góc xen giữa hai cạnh đó bằng
Câu hỏi:
Vẽ hình bình hành, biết hai cạnh liên tiếp bằng 3 cm, 4 cm và góc xen giữa hai cạnh đó bằng 60o. Hãy mô tả cách vẽ và giải thích tại sao hình vẽ được là hình bình hành.
Trả lời:
Giả sử hình bình hành ABCD có AD = 3cm, AB = 4 cm và .
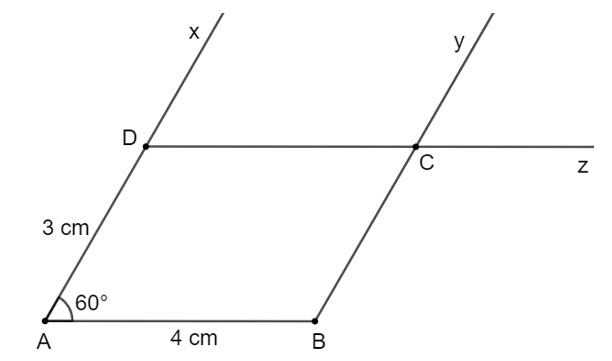
Cách vẽ:
- Vẽ cạnh AB = 4 cm.
- Vẽ . Trên tia Ax lấy điểm D sao cho AD = 3cm.
- Kẻ By // AD, Dz // BC. Hai tia By và Dz cắt nhau tại C, ta được hình bình hành ABCD.
Hình vẽ được là hình bình hành vì có hai cặp cạnh đối song song (AB // CD, AD // BC).