Cho tam giác ABC cân tại A có AB = 15 cm, BC = 10 cm, đường phân giác trong của góc
Câu hỏi:
Cho tam giác ABC cân tại A có AB = 15 cm, BC = 10 cm, đường phân giác trong của góc B cắt AC tại D. Khi đó, đoạn thẳng AD có độ dài là
A. 3 cm.
B. 6 cm.
C. 9 cm.
D. 12 cm.
Trả lời:
Đáp án đúng là: C
Vì tam giác ABC cân tại A nên AB = AC = 15 cm.
Theo đề bài, BD là tia phân giác của , áp dụng tính chất đường phân giác vào tam giác ABC, ta có:
suy ra .
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
.
Do đó AD = 3 . 3 = 9 (cm).
Vậy AD = 9 cm.
Xem thêm lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết:
Câu 1:
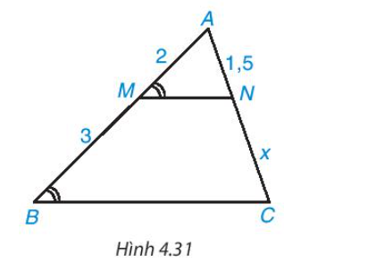
Độ dài x trong Hình 4.31 bằng
A. 2,75
B. 2.
C. 2,25.
D. 3,75.
Xem lời giải »
Câu 2:
Cho tam giác ABC. Gọi H, K lần lượt là trung điểm của AC, BC. Biết HK = 3,5 cm. Độ dài AB bằng
A. 3,5 cm.
B. 7 cm.
C. 10 cm.
D. 15 cm.
Xem lời giải »
Câu 3:
Cho tam giác ABC có chu vi là 32 cm. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Chu vi của tam giác MNP là
A. 8 cm.
B. 64 cm.
C. 30 cm.
D. 16 cm.
Xem lời giải »
Câu 4:
Cho tam giác ABC có AB = 9 cm, D là điểm thuộc cạnh AB sao cho AD = 6 cm. Kẻ DE song song với BC (E thuộc AC), kẻ EF song song với CD (F thuộc AB). Độ dài AF bằng
A. 4 cm.
B. 5 cm.
C. 6 cm.
D. 7 cm.
Xem lời giải »
Câu 5:
Cho góc xOy. Trên tia Ox, lấy hai điểm A và B sao cho OA = 2 cm, OB = 5 cm. Trên tia Oy, lấy điểm C sao cho OC = 3 cm. Từ điểm B kẻ đường thẳng song song với AC cắt Oy tại D. Tính độ dài đoạn thẳng CD.
Xem lời giải »
Câu 6:
Cho tam giác ABC vuông tại A. Gọi D, E, F lần lượt là trung điểm của AB, BC, AC.
a) Chứng minh rằng AE = DF.
Xem lời giải »
Câu 7:
b) Gọi I là trung điểm của DE. Chứng minh rằng ba điểm B, I, F thẳng hàng.
Xem lời giải »
Câu 8:
Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau tại G. Gọi I, K lần lượt là trung điểm của GB, GC. Chứng minh tứ giác EDKI là hình bình hành.
Xem lời giải »