Cho tia phân giác At của góc xAy (H.4.20). Nếu lấy điểm B trên tia Ax, điểm C trên tia Ay

Câu hỏi:

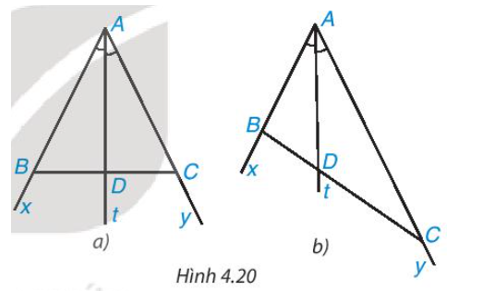
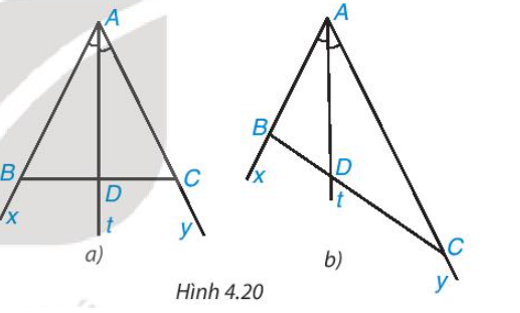
Cho tia phân giác At của góc xAy (H.4.20). Nếu lấy điểm B trên tia Ax, điểm C trên tia Ay, ta được tam giác ABC. Giả sử tia phân giác At cắt BC tại điểm D.

Cho tia phân giác At của góc xAy (H.4.20). Nếu lấy điểm B trên tia Ax, điểm C trên tia Ay (ảnh 1)

Khi lấy B và C sao cho AB = AC (H.4.20a), hãy so sánh tỉ số

\frac{D B}{D C}

và

\frac{A B}{A C}

Trả lời:

Theo đề bài, At là tia phân giác của góc xAy hay AD là tia phân giác của góc BAC.

Tam giác ABC cân tại A (vì AB = AC) có AD là tia phân giác của góc BAC nên AD cũng là đường trung tuyến của tam giác ABC.

Suy ra D là trung điểm của cạnh BC hay DB = DC nên $\frac{D B}{D C} = 1$ .

Vì AB = AC nên $\frac{A B}{A C} = 1$ .

Vậy khi lấy B và C sao cho AB = AC thì $\frac{D B}{D C} = \frac{A B}{A C}$ .

Xem thêm lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết:

Câu 1:

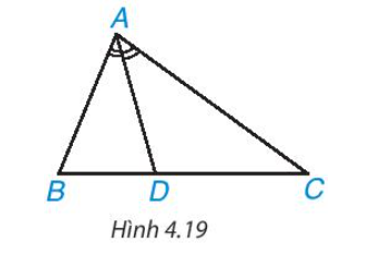
Trong H.4.19, AD là đường phân giác của tam giác ABC. Hai tỉ số $\frac{D B}{D C}$ và $\frac{A B}{A C}$ có bằng nhau không?

Trong H.4.19, AD là đường phân giác của tam giác ABC. Hai tỉ số DB/ DC và AB/AC có bằng nhau không? (ảnh 1)

Xem lời giải »

Câu 2:

Cho tia phân giác At của góc xAy (H.4.20). Nếu lấy điểm B trên tia Ax, điểm C trên tia Ay, ta được tam giác ABC. Giả sử tia phân giác At cắt BC tại điểm D

Khi lấy B và C sao cho AB = 2 cm và AC = 4 cm (H.4.20b), hãy dùng thước có vạch chia đến milimét để đo độ dài các đoạn thẳng DB, DC rồi so sánh hai tỉ số $\frac{D B}{D C}$ và $\frac{A B}{A C}$ .

Xem lời giải »

Câu 3:

Tính độ dài x trên Hình 4.23

Xem lời giải »

Câu 4:

Tính độ dài x trên Hình 4.24.

Xem lời giải »

Câu 5:

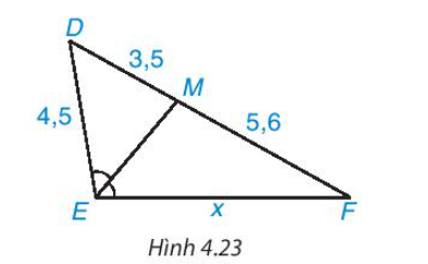
Cho tam giác ABC. Đường phân giác trong của góc A cắt BC tại D. Tính độ dài đoạn thẳng DC biết AB = 4,5 m; AC = 7,0 m và CB = 3,5 m (làm tròn kết quả đến hàng phần chục).

Xem lời giải »

❮ Bài trước Bài sau ❯