Chứng minh rằng các trung điểm của bốn cạnh trong một hình thoi là các đỉnh của một hình chữ nhật.
Câu hỏi:
Chứng minh rằng các trung điểm của bốn cạnh trong một hình thoi là các đỉnh của một hình chữ nhật.
Trả lời:
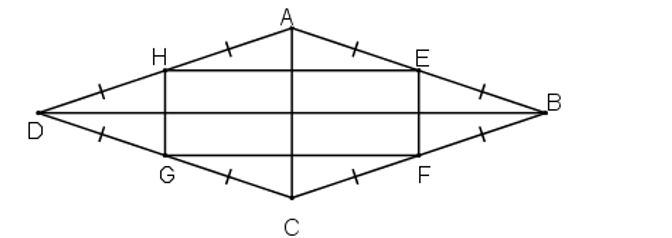
Xét tam giác ABC có E và F lần lượt là trung điểm của AB và BC.
Suy ra EF là đường trung bình của tam giác ABC.
Do đó EF // AC và (1)
* Tương tự tam giác ADC có HG là đường trung bình nên:
HG // AC và (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG.
Suy ra tứ giác EFGH là hình bình hành.
Lại có: EF // AC và BD ⊥ AC nên BD ⊥ EF.
EH // BD và EF ⊥ BD nên EF ⊥ EH.
Nên .
Hình bình hành EFGH có nên là hình chữ nhật.