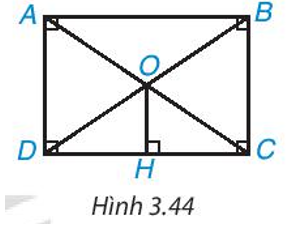
Hai thanh tre thẳng bằng nhau, được gắn với nhau tại trung điểm của mỗi thanh. Khi các đầu mút
Câu hỏi:
Hai thanh tre thẳng bằng nhau, được gắn với nhau tại trung điểm của mỗi thanh. Khi các đầu mút của hai thanh tre đó tạo thành bốn đỉnh của một tứ giác (H.3.40) thì tứ giác đó là hình gì? Tại sao?
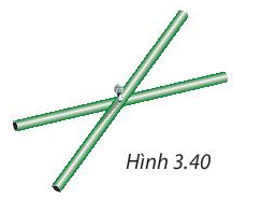
Trả lời:
Sau bài học này ta giải quyết được bài toán như sau:
Hai đầu mút của hai thanh tre tạo thành bốn đỉnh của tứ giác.
Tứ giác đó có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường nên tứ giác đó là hình chữ nhật.
Vậy khi các đầu mút của hai thanh tre đó tạo thành bốn đỉnh của một tứ giác thì tứ giác đó là hình chữ nhật.