Giải Toán 8 trang 33 Tập 1 Kết nối tri thức

---

Với Giải Toán 8 trang 33 Tập 1 trong Bài 6: Hiệu hai bình phương. Bình phương của một tổng hay một hiệu Toán lớp 8 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 trang 33.

Giải Toán 8 trang 33 Tập 1 Kết nối tri thức

Bài 2.1 trang 33 Toán 8 Tập 1: Những đẳng thức nào sau đây là hằng đẳng thức?

a) x + 2 = 3x + 1;

b) 2x(x + 1) = 2x² + 2x;

c) (a + b)a = a² + ba;

d) a – 2 = 2a + 1.

Lời giải:

a) Đẳng thức x + 2 = 3x + 1 không phải là hằng đẳng thức vì khi x = 0 thì kết quả ở vế trái bằng 2, vế phải bằng 1, khi đó kết quả của hai vế không bằng nhau;

b) Đẳng thức 2x(x + 1) = 2x² + 2x là hằng đẳng thức;

c) Đẳng thức (a + b)a = a² + ba là hằng đẳng thức;

d) Đẳng thức a – 2 = 2a + 1 không phải là hằng đẳng thức vì khi x = 2 thì kết quả ở vế trái bằng 0, vế phải bằng 5, khi đó kết quả của hai vế không bằng nhau.

Bài 2.2 trang 33 Toán 8 Tập 1: Thay bằng biểu thức thích hợp.

a) (x-3y)(x+3y) = x² - ;

b) (2x-y)(2x+y) = 4 - y²;

c) x² + 8xy + = ( + 4y)²;

d) - 12xy + 9y² = (2x - )².

Lời giải:

a) Ta có (x – 3y)(x + 3y) = x² – (3y)² = x² – 9y².

Vậy ta điền như sau (x-3y)(x+3y) = x² - ;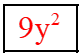

b) Ta có (2x – y)(2x + y) = (2x)² – y² = 4x² – y².

Vậy ta điền như sau (2x – y)(2x + y) = 4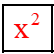 – y² ;

c) Ta có x² + 8xy + 16y² = x² + 2 . x . 4y + (4y)² = (x + 4y)².

Vậy ta điền như sau x² + 8xy + 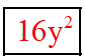= ( + 4y)² ;

d) Ta có 4x² – 12xy + 9y² = (2x)² – 2 . 2x . 3y + (3y)² = (2x – 3y)².

Vậy ta điền như sau 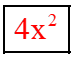– 12xy + 9y² = (2x – )² .

Bài 2.3 trang 33 Toán 8 Tập 1: Tính nhanh:

a) 54 . 66;

b) 203².

Lời giải:

a) 54 . 66 = (60 – 6)(60 + 6) = 60² – 6²

= 3 600 – 36 = 3564;

b) 203² = (200 + 3)² = 200² + 2 . 200 . 3 + 3²

= 40 000 + 1 200 + 9 = 41 209.

Bài 2.4 trang 33 Toán 8 Tập 1: Viết các biểu thức sau dưới dạng bình phương của một tổng hoặc một hiệu:

a) x² + 4x + 4;

b) 16a² – 16ab + 4b².

Lời giải:

a) x² + 4x + 4 = x² + 2 . x . 2 + 2² = (x + 2)²;

b) 16a² – 16ab + 4b² = (4a)² – 2 . 4a . 2b + (2b)² = (4a – 2b)².

Bài 2.5 trang 33 Toán 8 Tập 1: Rút gọn các biểu thức sau:

a) (x – 3y)² – (x + 3y)²;

b) (3x + 4y)² + (4x – 3y)².

Lời giải:

a) (x – 3y)² – (x + 3y)² = [(x – 3y) + (x + 3y)] [(x – 3y) – (x + 3y)]

= (x – 3y + x + 3y)(x – 3y – x – 3y) = 2x . (–6y) = –12xy;

b) (3x + 4y)² + (4x – 3y)²

= (3x)² + 2 . 3x . 4y + (4y)² + (4x)² – 2 . 4x . 3y + (3y)²

= (3x)² + (4y)² + (4x)² + (3y)² = 9x² + 16y² + 16x² + 9y²

= 25x² + 25y².

Bài 2.6 trang 33 Toán 8 Tập 1: Chứng minh rằng với mọi số tự nhiên n, ta có:

(n + 2)² – n² chia hết cho 4.

Lời giải:

Ta có (n + 2)² – n² = (n + 2 – n)(n + 2 + n) = 2(2n + 2) = 4n + 4 = 4(n + 1)

Vì n là số tự nhiên nên n + 1 cũng là số tự nhiên

Và 4 ⋮ 4 nên 4(n + 1) ⋮ 4.

Vậy với mọi số tự nhiên n, ta có (n + 2)² – n² chia hết cho 4.

Lời giải bài tập Toán 8 Bài 6: Hiệu hai bình phương. Bình phương của một tổng hay một hiệu Kết nối tri thức hay khác:

• Giải Toán 8 trang 30

• Giải Toán 8 trang 31

• Giải Toán 8 trang 32