Giải Toán 8 trang 47 Tập 1 Kết nối tri thức

---

Với Giải Toán 8 trang 47 Tập 1 trong Bài tập cuối chương 2 Toán lớp 8 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 trang 47.

Giải Toán 8 trang 47 Tập 1 Kết nối tri thức

Bài 2.28 trang 47 Toán 8 Tập 1: Đa thức x² – 9x + 8 được phân tích thành tích của hai đa thức

A. x – 1 và x + 8;

B. x – 1 và x – 8;

C. x – 2 và x – 4;

D. x – 2 và x + 4.

Lời giải:

Đáp án đúng là: B

Ta có x² – 9x + 8 = (x² – x) – (8x – 8)

= x(x – 1) – 8(x – 1) = (x – 1)(x – 8).

Do đó, đa thức x² – 9x + 8 được phân tích thành tích của hai đa thức x – 1 và x – 8.

Bài 2.29 trang 47 Toán 8 Tập 1: Khẳng định nào sau đây là đúng?

A. (A – B)(A + B) = A² + 2AB + B²;

B. (A + B)(A – B) = A² – 2AB + B²;

C. (A + B)(A – B) = A² + B²;

D. (A + B)(A – B) = A² – B².

Lời giải:

Đáp án đúng là: D

Ta có (A – B)(A + B) = (A + B)(A – B) = A² – B².

Bài 2.30 trang 47 Toán 8 Tập 1: Biểu thức 25x² + 20xy + 4y² viết dưới dạng bình phương của một tổng là:

A. [5x+(-2y)]²;

B. [2x+(-5y)]²;

C. (2x + 5y)²;

D. (5x + 2y)².

Lời giải:

Đáp án đúng là: D

Ta có 25x² + 20xy + 4y² = (5x)² + 2 . 5x . 2y + (2y)²

= (5x + 2y)².

Bài 2.31 trang 47 Toán 8 Tập 1: Rút gọn biểu thức A = (2x + 1)³ – 6x(2x + 1) ta được:

A. x³ + 8;

B. x³ + 1;

C. 8x³ + 1;

D. 8x³ – 1.

Lời giải:

Đáp án đúng là: C

Ta có A = (2x + 1)³ – 6x(2x + 1)

= (2x)³ + 3 . (2x)² . 1 + 3 . 2x . 1² + 1³ – 12x² – 6x

= 8x³ + 12x² + 6x + 1 – 12x² – 6x = 8x³ + 1.

Bài 2.32 trang 47 Toán 8 Tập 1: Tính nhanh giá trị của các biểu thức:

a) x² – 4x + 4 tại x = 102;

b) x³ + 3x² + 3x + 1 tại x = 999.

Lời giải:

a) Ta có x² – 4x + 4 = (x – 2)²

Thay x = 102 vào biểu thức (x – 2)², ta được:

(102 – 2)² = 100² = 10 000.

b) Ta có x³ + 3x² + 3x + 1 = (x + 1)³.

Thay x = 999 vào biểu thức (x + 1)³, ta được:

(999 + 1)³ = 1000³ = 1 000 000 000.

Bài 2.33 trang 47 Toán 8 Tập 1: Rút gọn các biểu thức:

a) (2x – 5y)(2x + 5y) + (2x + 5y)²;

b) (x + 2y)(x² – 2xy + 4y²) + (2x – y)(4x² + 2xy + y²).

Lời giải:

a) (2x – 5y)(2x + 5y) + (2x + 5y)²

= 4x² – 25y² + 4x² + 20xy + 25y²

= 8x² + 20xy.

b) (x + 2y)(x² – 2xy + 4y²) + (2x – y)(4x² + 2xy + y²)

= (x + 2y)[x² – x . 2y + (2y)²] + (2x – y)[(2x)² + 2x . y + y²]

= (x + 2y)[x² – x . 2y + (2y)²] + (2x – y)[(2x)² + 2x . y + y²]

= x³ + (2y)³ + (2x)³ – y³

= x³ + 8y³ + 8x³ – y³

= 9x³ + 7y³.

Bài 2.34 trang 47 Toán 8 Tập 1: Phân tích các đa thức sau thành thành nhân tử:

a) 6x² – 24y²;

b) 64x³ – 27y³;

c) x⁴ – 2x³ + x²;

d) (x – y)³ + 8y³.

Lời giải:

a) 6x² – 24y² = 6(x² – 4y²) = 6(x + 2y)(x – 2y);

b) 64x³ – 27y³ = (4x)³ – (3y)³ = (4x – 3y)[(4x)² + 4x . 3y + (3y)²]

= (4x – 3y)(16x² + 12xy + 9y²);

c) x⁴ – 2x³ + x² = x²(x² – 2x + 1) = x²(x – 1)²;

d) (x – y)³ + 8y³ = (x – y)³ + (2y)³

= (x – y + 2y)[(x – y)² – (x – y) . 2y + (2y)²]

= (x + y)(x² – 2xy + y² – 2xy + 2y² + 4y²)

= (x + y)(x² – 4xy + 7y²).

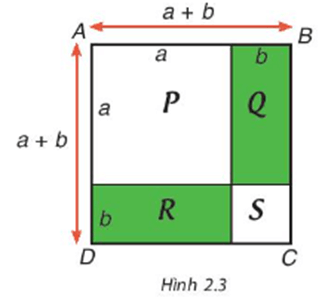
Bài 2.35 trang 47 Toán 8 Tập 1: Sử dụng Hình 2.3, bằng cách tính diện tích hình vuông ABCD theo hai cách, hãy giải thích hằng đẳng thức (a + b)² = a² + 2ab + b².

Lời giải:

Cách 1. Tính diện tích hình vuông ABCD có độ dài một cạnh bằng a + b.

Diện tích hình vuông ABCD là: (a + b)²

Cách 2. Tính diện tích hình vuông ABCD bằng tổng diện tích các hình P, Q, R, S.

Diện tích hình vuông P là: a²;

Diện tích hình hình chữ nhật Q là: ab;

Diện tích hình hình chữ nhật R là: ab;

Diện tích hình vuông S là: b²;

Diện tích hình vuông ABCD là: a² + ab + ab + b² = a² + 2ab + b².

Từ hai cách tính diện tích hình vuông ABCD ở trên, ta có: (a + b)² = a² + 2ab + b².