Giải Toán 8 trang 80 Tập 1 Kết nối tri thức

---

Với Giải Toán 8 trang 80 Tập 1 trong Bài 15: Định lí Thalès trong tam giác Toán lớp 8 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 trang 80.

Giải Toán 8 trang 80 Tập 1 Kết nối tri thức

Vận dụng trang 80 Toán 8 Tập 1: Em hãy trả lời câu hỏi trong tình huống mở đầu.

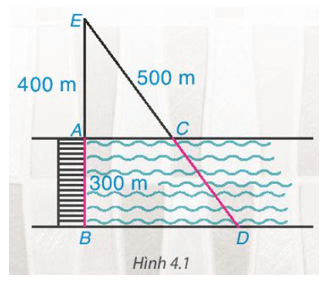
Cây cầu AB bắc qua một con sông có chiều rộng 300 m. Để đo khoảng cách giữa hai điểm C và D trên hai bờ con sông, người ta chọn một điểm E trên đường thẳng AB sao cho ba điểm E, C, D thẳng hàng. Trên mặt đất, người ta đo được AE = 400 m, EC = 500 m. Theo em, người ta tính khoảng cách giữa C và D như thế nào?

Lời giải:

Hai cạnh AC và BD thuộc hai bờ của con sông nên AC // BD, áp dụng định lí Thalès, ta có:

$\frac{AE}{AB}=\frac{CE}{CD}$ hay $\frac{400}{300}=\frac{500}{CD}$.

Suy ra $CD=\frac{300.500}{400}=375$ (m).

Vậy khoảng cách giữa C và D bằng 375 m.

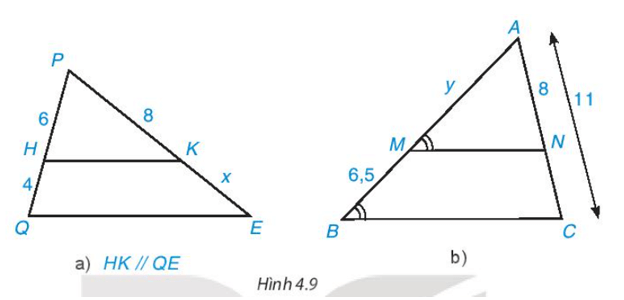
Bài 4.1 trang 80 Toán 8 Tập 1: Tìm độ dài x, y trong Hình 4.9 (làm tròn kết quả đến chữ số thập phân thứ nhất).

Lời giải:

• Hình 4.9a)

Vì HK // QE nên áp dụng định lí Thalès, ta có:

$\frac{PH}{QH}=\frac{PK}{KE}$ hay $\frac{6}{4}=\frac{8}{x}$ .

Suy ra $x=\frac{8.4}{6}=\frac{16}{3}\approx \mathrm{5,3}$  (đvđd).

• Hình 4.9b)

Vì $\widehat{AMN}=\widehat{ABC}$ mà $\widehat{AMN}$ và $\widehat{ABC}$ là hai góc đồng vị nên MN // BC.

Ta có AB = AM + BM = y + 6,5.

Áp dụng định lí Thalès, ta có: $\frac{AM}{AB}=\frac{AN}{AC}$  hay $\frac{y}{y+\mathrm{6,5}}=\frac{8}{11}$ .

Suy ra 11y = 8(y + 6,5)

11y = 8y + 52

11y – 8y = 52

3y = 52

$y=\frac{52}{3}\approx \mathrm{17,3}$(đvđd)

Vậy x ≈ 5,3 (đvđd); y ≈ 17,3 (đvđd).

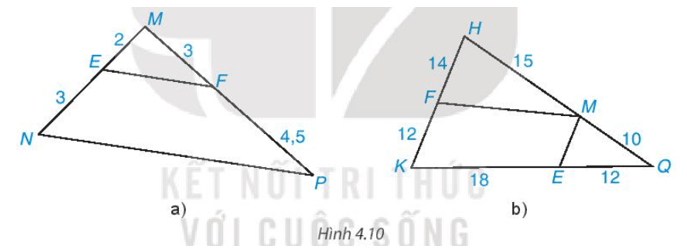
Bài 4.2 trang 80 Toán 8 Tập 1: Tìm các cặp đường thẳng song song trong Hình 4.10 và giải thích tại sao chúng song song với nhau.

Lời giải:

• Hình 4.10a)

Ta có $\frac{EM}{EN}=\frac{2}{3};\frac{MF}{PF}=\frac{3}{\mathrm{4,5}}=\frac{2}{3}$  nên $\frac{EM}{EN}=\frac{MF}{PF}$ .

Vì $\frac{EM}{EN}=\frac{MF}{PF}$ , E ∈ MN, F ∈ MP nên theo định lí Thalès đảo ta suy ra EF // NP.

• Hình 4.10b)

* Ta có: $\frac{HF}{KF}=\frac{14}{12}=\frac{7}{6};\frac{HM}{MQ}=\frac{15}{10}=\frac{3}{2}$ .

Vì $\frac{HF}{KF}\ne \frac{HM}{MQ}$ nên MF không song song với KQ.

* Ta có: $\frac{MQ}{MH}=\frac{10}{15}=\frac{2}{3};\frac{EQ}{EK}=\frac{12}{18}=\frac{2}{3}$ .

Vì $\frac{MQ}{MH}=\frac{EQ}{EK}$ ; E ∈ KQ; M ∈ HQ HQ nên theo định lí Thalès đảo ta suy ra ME // HK.

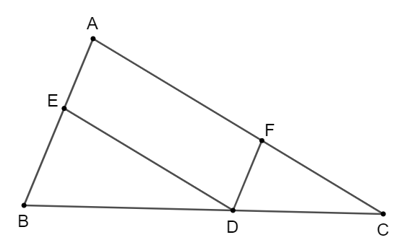
Bài 4.3 trang 80 Toán 8 Tập 1: Cho ∆ABC, từ điểm D trên cạnh BC, kẻ đường thẳng song song với AB cắt AC tại F và kẻ đường thẳng song song với AC cắt AB tại E.

Chứng minh rằng: $\frac{AE}{AB}+\frac{AF}{AC}=1$.

Lời giải:

Áp dụng định lí Thalès, ta có:

• Vì DE // AC nên $\frac{AE}{AB}=\frac{CD}{BC}$;

• Vì DF // AC nên $\frac{AF}{AC}=\frac{BD}{BC}$.

Khi đó, $\frac{AE}{AB}+\frac{AF}{AC}$ = $\frac{CD}{BC}+\frac{BD}{BC}$ = $\frac{BC}{BC}$ = 1

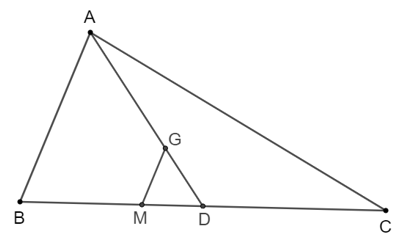
Bài 4.4 trang 80 Toán 8 Tập 1: Cho ∆ABC có trọng tâm G. Vẽ đường thẳng d qua G và song song với AB, d cắt BC tại điểm M. Chứng minh rằng $BM=\frac{1}{3}BC$

Lời giải:

Lấy D là trung điểm của cạnh BC.

Khi đó, AD là đường trung tuyến của tam giác ABC.

Vì G là trọng tâm của tam giác ABC nên điểm G nằm trên cạnh AD.

Ta có $\frac{AG}{AD}=\frac{2}{3}$ hay $AG=\frac{2}{3}AD$.

Vì MG // AB, theo định lí Thalès, ta suy ra: $\frac{AG}{AD}=\frac{BM}{BD}=\frac{2}{3}$.

Ta có BD = CD (vì D là trung điểm của cạnh BC) nên $\frac{BM}{BC}=\frac{BM}{2BD}=\frac{2}{2.3}=\frac{1}{3}$.

Do đó $BM=\frac{1}{3}BC$ (đpcm).

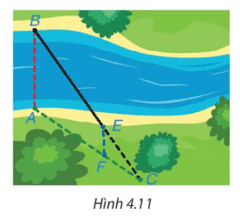
Bài 4.5 trang 80 Toán 8 Tập 1: Để đo khoảng cách giữa hai vị trí B và E ở hai bên bờ sông, bác An chọn ba vị trí A, F, C cùng nằm ở một bên bờ sông sao cho ba điểm C, E, B thẳng hàng, ba điểm C, F, A thẳng hàng và AB // EF (H.4.11). Sau đó bác An đo được AF = 40 m, FC = 20 m, EC = 30 m. Hỏi khoảng cách giữa hai vị trí B và E bằng bao nhiêu?

Lời giải:

Theo đề bài, ba điểm C, E, B thẳng hàng, ba điểm C, F, A thẳng hàng và AB // EF, áp dụng định lí Thalès, ta có:

$\frac{EC}{BE}=\frac{CF}{AF}$ hay $\frac{30}{BE}=\frac{20}{40}$ .

Suy ra $BE=\frac{30.40}{20}=60$  (m).

Vậy khoảng cách giữa hai vị trí B và E bằng 60 m.

Lời giải bài tập Toán 8 Bài 15: Định lí Thalès trong tam giác hay khác:

• Giải Toán 8 trang 77
• Giải Toán 8 trang 79