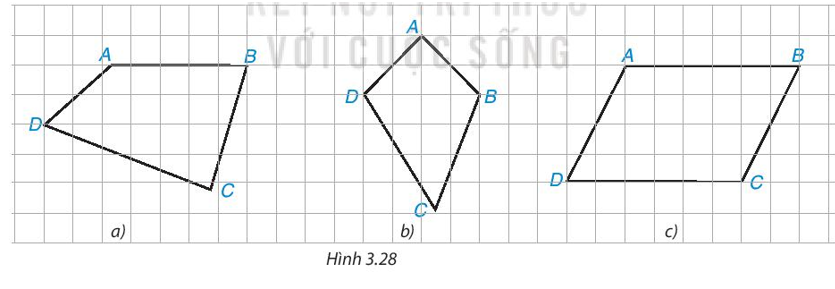
Trong mỗi trường hợp sau đây, tứ giác nào là hình bình hành, tứ giác nào không là hình bình hành? Vì sao?
Câu hỏi:
Trong mỗi trường hợp sau đây, tứ giác nào là hình bình hành, tứ giác nào không là hình bình hành? Vì sao?
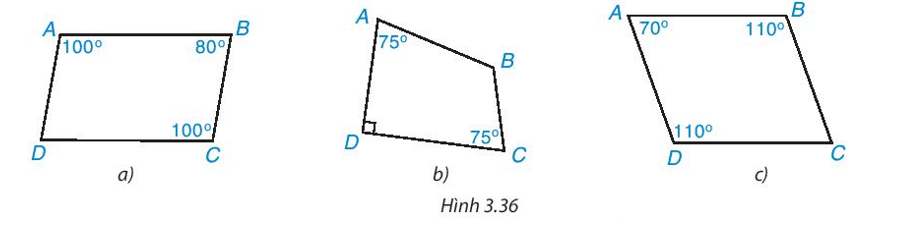
Trả lời:
* Hình 3.36a)
Xét tứ giác ABCD có: .
Suy ra .
Tứ giác ABCD có: ; .
Do đó, tứ giác ABCD là hình bình hành.
* Hình 3.36b)
Xét tứ giác ABCD có: .
Suy ra .
Tứ giác ABCD có: nhưng .
Do đó, tứ giác ABCD không là hình bình hành.
* Hình 3.36c)
Xét tứ giác ABCD có: .
Suy ra .
Tứ giác ABCD có: ; .
Do đó, tứ giác ABCD là hình bình hành.
Vậy tứ giác ABCD trong Hình 3.36a) và 3.36c) là hình bình hành; tứ giác ABCD trong Hình 3.36b) không là hình bình hành.