Câu hỏi:
Xét một điểm M trên cạnh huyền của tam giác ABC vuông cân tại A. Gọi N và P lần lượt là hình chiếu vuông góc của M trên các cạnh AB và AC.
a) Hỏi tứ giác MPAN là hình gì?
Trả lời:
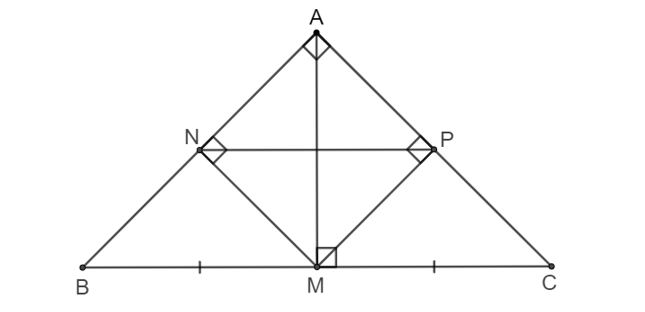
a) Tứ giác MPAN có:
Suy ra .
Tứ giác MPAN có: .
Do đó tứ giác MPAN là hình chữ nhật.
Câu 1:
Hai thanh tre thẳng bằng nhau, được gắn với nhau tại trung điểm của mỗi thanh. Khi các đầu mút của hai thanh tre đó tạo thành bốn đỉnh của một tứ giác (H.3.40) thì tứ giác đó là hình gì? Tại sao?
Câu 3:
Hình chữ nhật có là hình bình hành không, có là hình thang cân không? Tại sao?
Ta có tính chất sau đây về đường chéo của hình chữ nhật.
Câu 4:
Cho hình chữ nhật ABCD. Hai đường chéo AC, BD cắt nhau tại O. Kẻ OH ⊥ DC (H.3.44). Chứng minh rằng H là trung điểm của DC.
