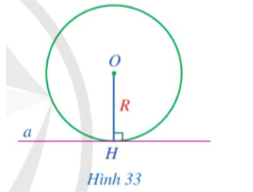
Cho đường thẳng a và đường tròn (O; R) thỏa mãn đường thẳng a đi qua điểm H thuộc đường tròn (O; R) và a ⊥ OH (Hình 35).
Câu hỏi:
Cho đường thẳng a và đường tròn (O; R) thỏa mãn đường thẳng a đi qua điểm H thuộc đường tròn (O; R) và a ⊥ OH (Hình 35).
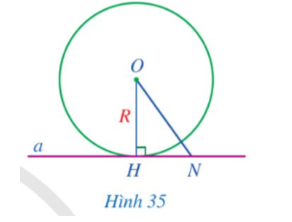
a) So sánh khoảng cách từ điểm O đến đường thẳng a và bán kính R.
b) Giả sử N là điểm thuộc đường thẳng a và N khác H. So sánh ON và R. Điểm N có thuộc đường tròn (O; R) hay không?
c) Đường thẳng a có phải là tiếp tuyến của đường tròn (O; R) hay không?
Trả lời:
a) Vì OH ⊥ a tại H nên khoảng cách từ điểm O đến đường thẳng a là OH = R.
b) Ta có ON, OH lần lượt là đường xiên và đường vuông góc kẻ từ O đến đường thẳng a nên ON > OH hay ON > R.
Do đó điểm N nằm ngoài đường tròn (O; R).
c) Ta có a vuông góc với bán kính OH tại điểm H nên a là tiếp tuyến của đường tròn (O; R) tại tiếp điểm H.