Chứng minh trong một đường tròn: a) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy;
Câu hỏi:
Chứng minh trong một đường tròn:
a) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy;
Trả lời:
a)
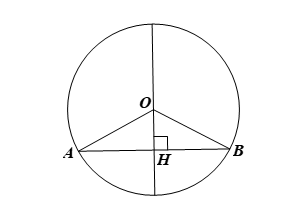
Gọi (O) là đường tròn có đường kính vuông góc với dây AB tại H.
Xét ∆OAB có OA = OB = R nên ∆OAB cân tại O.
∆OAB cân tại O có OH là đường cao (do OH ⊥ AB) nên đồng thời là đường trung tuyến của tam giác. Do đó H là trung điểm của AB.
Vậy đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.