Giải Toán 9 trang 110 Tập 1 Cánh diều
Với Giải Toán 9 trang 110 Tập 1 trong Bài 3: Tiếp tuyến của đường tròn Toán lớp 9 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 110.
Giải Toán 9 trang 110 Tập 1 Cánh diều
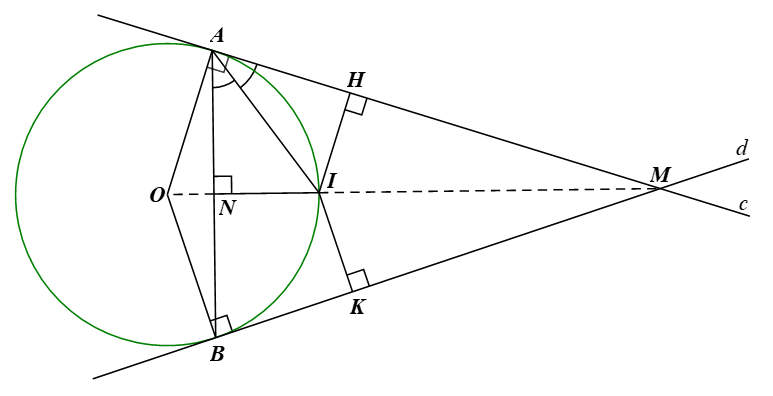
Bài 3 trang 110 Toán 9 Tập 1: Cho đường tròn (O) và điểm M nằm ngoài đường tròn. Hai đường thẳng c, d đi qua M lần lượt tiếp xúc với (O) tại A, B. Tia phân giác của góc MAB cắt MO tại I. Chứng minh điểm I cách đều ba đường thẳng MA, MB và AB.
Lời giải:
Gọi H, K và N lần lượt là hình chiếu của I lên MA, MA và AB.
Theo cách vẽ, ta có IH ⊥ MA, IK ⊥ MB, IN ⊥ AB nên
Xét ∆ANI (vuông tại N) và ∆AHI (vuông tại H) có:
AI là cạnh chung; (do AI là phân giác của ).
Do đó ∆ANI = ∆AHI (cạnh huyền – góc nhọn).
Suy ra IN = IH (hai cạnh tương ứng). (1)
Vì MA, MB là hai tiếp tuyến của đường tròn (O) cắt nhau tại M với A, B là các tiếp điểm nên MO là tia phân giác của hay MI là tia phân giác của
Xét ∆MHI (vuông tại H) và ∆MKI (vuông tại K) có:
MI là cạnh chung và (do MI là tia phân giác của ).
Do đó ∆MHI = ∆MKI (cạnh huyền – góc nhọn).
Suy ra IH = IK (hai cạnh tương ứng). (2)
Từ (1) và (2) suy ra IN = IH = IK.
Vậy điểm I cách đều ba đường thẳng MA, MB và AB.
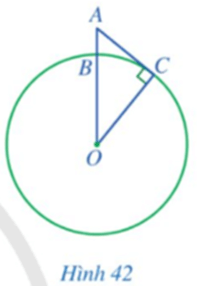
Bài 4 trang 110 Toán 9 Tập 1: Một người quan sát đặt mắt ở vị trí A có độ cao cách mực nước biển là AB = 5 m. Cắt bề mặt Trái Đất bởi một mặt phẳng đi qua điểm A và tâm Trái Đất thì phần chung giữa chúng là một đường tròn lớn tâm O. Tầm quan sát tối đa từ vị trí A là đoạn thẳng AC, trong đó C là tiếp điểm của tiếp tuyến đi qua A với đường tròn (O) (minh họa như Hình 42). Tính độ dài của đoạn thẳng AC (theo đơn vị kilômét và làm tròn kết quả đến hàng phần mười), biết bán kính Trái Đất là OB = OC ≈ 6 400 km.
(Nguồn: Toán 9 – Tập một, NXB Giáo dục Việt Nam, năm 2017)
Lời giải:
Theo bài, ta có: AB = 5 m = 0,005 km.
Khi đó, OA = OB + AB ≈ 6 400 + 0,005 = 6 400,005 (km).
Vì AC là tiếp tuyến của đường tròn (O) nên AC ⊥ OC tại C, hay
Do đó ∆OAC vuông tại C.
Theo định lí Pythagore, ta có:
OA2 = OC2 + AC2
Suy ra AC2 = OA2 – OC2 ≈ 6 400,0052 – 6 4002 = 64,000025.
Do đó
Vậy AC ≈ 8,0 km.
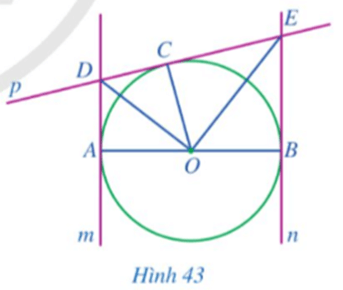
Bài 5 trang 110 Toán 9 Tập 1: Cho đường tròn (O; R) đường kính AB và các đường thẳng m, n, p lần lượt tiếp xúc với đường tròn tại A, B, C (Hình 43).
Chứng minh:
a) AD + BE = DE;
b) và
c) Tam giác ODE vuông.
d)
Lời giải:
a) Vì DA, DC là hai tiếp tuyến của đường tròn (O) cắt nhau tại D nên DA = DC (tính chất hai tiếp tuyến cắt nhau).
Vì EB, EC là hai tiếp tuyến của đường tròn (O) cắt nhau tại E nên EB = EC (tính chất hai tiếp tuyến cắt nhau).
Do đó DA + EB = DC + EC hay AD + BE = DE.
b) Vì DA, DC là hai tiếp tuyến của đường tròn (O) cắt nhau tại D nên OA là tia phân giác của (tính chất hai tiếp tuyến cắt nhau).
Do đó (tính chất tia phân giác).
Vì EB, EC là hai tiếp tuyến của đường tròn (O) cắt nhau tại E nên OE tia phân giác của (tính chất hai tiếp tuyến cắt nhau).
Do đó (tính chất tia phân giác).
c) Ta có:
Mà và (chứng minh ở câu b)
Do đó
Vậy tam giác ODE vuông tại O.
d) Vì DE là tiếp tuyến của đường tròn (O) tại C nên OC ⊥ DE tại C.
Xét ∆ODE và ∆CDO có:
và là góc chung
Do đó ∆ODE ᔕ ∆CDO (g.g)
Suy ra (tỉ số các cạnh tương ứng)
Nên CO = hay = R.
Lời giải bài tập Toán 9 Bài 3: Tiếp tuyến của đường tròn hay khác: