Giải Toán 9 trang 71 Tập 1 Cánh diều
Với Giải Toán 9 trang 71 Tập 1 trong Bài 4: Một số phép biến đổi căn thức bậc hai của biểu thức đại số Toán lớp 9 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 71.
Giải Toán 9 trang 71 Tập 1 Cánh diều
Bài 3 trang 71 Toán 9 Tập 1: Áp dụng quy tắc về căn thức bậc hai của một thương, hãy rút gọn biểu thức:
a) với a > 3;
b) với x > 0;
c) với x > 1;
d) với x ≥ 2.
Lời giải:
a) = 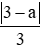
b) = |x| = x (vì x > 0).
c) = 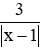
d) = 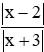
Bài 4 trang 71 Toán 9 Tập 1: Trục căn thức ở mẫu:
a)
b) với a > 0;
c)
d) với x > 0, x ≠ 9;
e)
g) với x > 0, x ≠ 3.
Lời giải:
a) Ta có:
b) Với a > 0, ta có
c) Ta có:
d) Với x > 0, x ≠ 9, ta có:
e) Ta có:
g) Với x > 0, x ≠ 3, ta có:
Bài 5 trang 71 Toán 9 Tập 1: Rút gọn biểu thức: với a ≥ 0, b ≥ 0, a ≠ b.
Lời giải:
Với a ≥ 0, b ≥ 0, a ≠ b, ta có:
Lời giải bài tập Toán 9 Bài 4: Một số phép biến đổi căn thức bậc hai của biểu thức đại số hay khác:
