Bài 4 trang 80 Toán 9 Tập 2 Chân trời sáng tạo

Cho đường tròn (O; R).

Giải Toán 9 Bài 3: Đa giác đều và phép quay - Chân trời sáng tạo

Bài 4 trang 80 Toán 9 Tập 2: Cho đường tròn (O; R).

a) Vẽ hình tam giác đều, hình vuông, hình lục giác đều có các đỉnh nằm trên (O; R).

b) Tính các cạnh của các hình vừa vẽ theo R.

Lời giải:

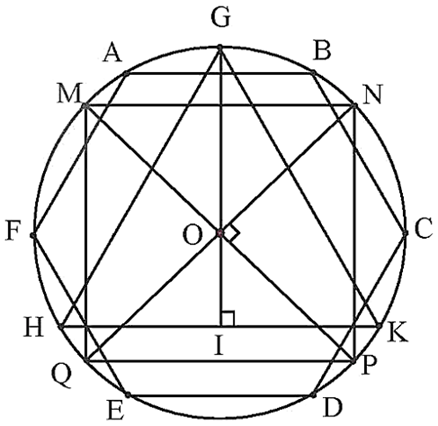
a) Hình tam giác đều GHK, hình vuông MNPQ, hình lục giác đều ABCDEF có các đỉnh nằm trên (O; R) được vẽ như hình dưới đây.

b) • Xét tam giác đều GHK.

Kẻ đường cao GI (I ∈ HK). Xét tam giác GIK vuông tại I, ta có:

GI = $\frac{3}{2}$GO = $\frac{3}{2}$R;

GI = GK . sin K, suy ra $GK=\frac{GI}{\sin K}=\frac{\frac{3}{2}R}{\frac{\sqrt{3}}{2}}=R\sqrt{3}.$

• Xét hình vuông MNPQ.

Tam giác NOP vuông tại O.

Theo định lí Pythagore, ta có: NP² = ON² + OP² = R² + R² = 2R².

Suy ra NP = R$\sqrt{2}$.

 • Xét hình lục giác đều ABCDEF.

Tam giác AOB có OA = OB và $\widehat{AOB}=\frac{360°}{6}=60°$ nên là tam giác AOB đều.

Suy ra AB = OA = OB = R.

Vậy cạnh của tam giác đều GHK là R$\sqrt{3}$, cạnh hình vuông MNPQ là R$\sqrt{2}$ và cạnh hình lục giác đều ABCDEF là R.

Lời giải bài tập Toán 9 Bài 3: Đa giác đều và phép quay hay, chi tiết khác:

• Khởi động trang 75 Toán 9 Tập 2: Trong mỗi đường gấp khúc khép kín nối các đỉnh của mỗi hình dưới đây ....

• Khám phá 1 trang 75 Toán 9 Tập 2: Có nhận xét gì về cạnh và góc của mỗi đa giác sau? ....

• Thực hành 1 trang 77 Toán 9 Tập 2: Cho đường tròn (O; R), trên đó lấy các điểm M, N, P, Q, R sao cho ....

• Vận dụng 1 trang 77 Toán 9 Tập 2: Cho lục giác đều ABCDEF có M, N, P, Q, R, S lần lượt là trung điểm ....

• Khám phá 2 trang 77 Toán 9 Tập 2: Vẽ hình vuông ABCD tâm O (Hình 5a). Cắt một tấm bìa hình vuông ....

• Thực hành 2 trang 78 Toán 9 Tập 2: Tìm phép quay biến hình ngũ giác đều tâm I thành chính nó (Hình 8) ....

• Vận dụng 2 trang 78 Toán 9 Tập 2: Một vòng quay may mắn có dạng hình đa giác đều 10 cạnh (Hình 9) ....

• Thực hành 3 trang 79 Toán 9 Tập 2: Em hãy tìm một số hình phẳng đều trong thực tế ....

• Bài 1 trang 79 Toán 9 Tập 2: Gọi tên đa giác đều trong mỗi hình sau và tìm các phép quay có thể biến mỗi hình dưới đây thành chính nó ....

• Bài 2 trang 79 Toán 9 Tập 2: Cho đa giác đều 9 cạnh có tâm O và AB, BC là hai cạnh đa giác (Hình 12) ....

• Bài 3 trang 80 Toán 9 Tập 2: Đường viền ngoài của chiếc đồng hồ trong Hình 13 được làm theo hình đa giác đều nào? ....

• Bài 5 trang 80 Toán 9 Tập 2: Tìm các hình phẳng có tính đều ....

• Bài 6 trang 80 Toán 9 Tập 2: Vòng trong của mái giếng trời hình hoa sen của nhà ga Bến Thành ....