Lý thuyết Toán 9 Cung và dây của một đường tròn - Kết nối tri thức

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 9 Bài 14: Cung và dây của một đường tròn sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 9 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán 9 Cung và dây của một đường tròn - Kết nối tri thức

Lý thuyết Cung và dây của một đường tròn

1. Dây và đường kính của đường tròn

1.1. Khái niệm dây và đường kính của đường tròn

⦁ Đoạn thẳng nối hai điểm tùy ý của một đường tròn gọi là một dây (hay dây cung) của đường tròn.

⦁ Mỗi dây đi qua tâm là một đường kính của đường tròn. Dễ thấy đường kính của đường tròn bán kính R có độ dài bằng 2R.

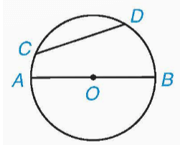
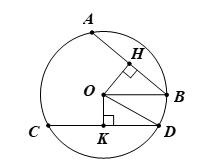
Chẳng hạn, trên hình vẽ dưới đây, CD là một dây, AB là một đường kính của (O).

1.2. Quan hệ giữa dây và đường kính

Định lí: Trong một đường tròn, đường kính là dây cung lớn nhất.

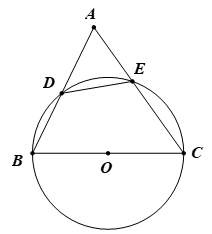
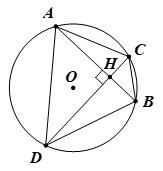
Ví dụ 1. Cho tam giác nhọn ABC. Đường tròn tâm O đường kính BC cắt các cạnh AB và AC lần lượt tại D và E. Chứng minh DE < BC.

Hướng dẫn giải

Ta thấy D, E nằm cùng một phía so với đường thẳng BC nên DE là một dây (không đi qua tâm) của đường tròn (O).

Áp dụng định lí trên, ta thu được DE < BC.

2. Góc ở tâm, cung và số đo của một cung

2.1. Khái niệm góc ở tâm và cung tròn

Cho hai điểm A và B cùng thuộc một đường tròn. Hai điểm ấy chia đường tròn thành hai phần, mỗi phần gọi là một cung tròn (hay cung). Hai điểm A và B gọi là hai mút (hay đầu mút) của mỗi cung đó.

Góc ở tâm là góc có đỉnh trùng với tâm của đường tròn.

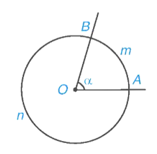
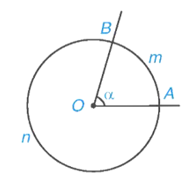
Trên hình vẽ dưới đây, ta có hai cung, kí hiệu là $\stackrel{⏜}{AmB}$và $\stackrel{⏜}{AnB}$nhưng chỉ có một góc ở tâm là $\widehat{AOB}$.

Chú ý:

⦁ Khi góc AOB không bẹt thì cung nằm trong góc AOB gọi là cung nhỏ (ở hình vẽ trên, $\stackrel{⏜}{AmB}$ là cung nhỏ). Khi đó $\stackrel{⏜}{AmB}$ còn có thể kí hiệu gọn là $\stackrel{⏜}{AB}$. Cung còn lại, $\stackrel{⏜}{AnB}$ gọi là cung lớn. Khi góc AOB bẹt thì mỗi cung AB được gọi là một nửa đường tròn.

⦁ Ta còn nói góc AOB chắn cung AB hay cung AB bị chắn bởi góc AOB.

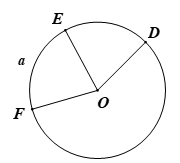
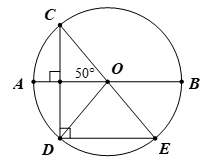
Ví dụ 2.Cho hình vẽ:

a) Tìm các cung có hai đầu mút là D, E.

b) $\stackrel{⏜}{EaF}$ bị chắn bởi góc ở tâm nào?

c) Góc ở tâm DOF chắn cung nào?

Hướng dẫn giải

a) Các cung có hai đầu mút D, E là: cung nhỏ $\stackrel{⏜}{DE}$ và $\stackrel{⏜}{DFE}$.

b) $\stackrel{⏜}{EaF}$ bị chắn bởi góc ở tâm EOF.

c) Góc ở tâm DOF chắn $\stackrel{⏜}{DFE}$.

2.2. Cách xác định số đo của một cung

Số đo của một cung được xác định như sau:

– Số đo của nửa đường tròn bằng 180°.

– Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.

– Số đo của cung lớn bằng hiệu giữa 360° và số đo của cung nhỏ có chung hai mút.

Số đo của cung AB được kí hiệu là sđ$\stackrel{⏜}{AB}$.

Trên hình vẽ, ta có:

sđ$\stackrel{⏜}{AmB}=\widehat{AOB}=\alpha$(0° < α ≤ 180°) và sđ$\stackrel{⏜}{AnB}=360°-\alpha$.

Chú ý:

⦁ Cung có số đo n° còn gọi là cung n°. Cả đường tròn được gọi là cung 360°. Đôi khi ta cũng coi một điểm là cung 0°.

⦁ Hai cung trên một đường tròn gọi là bằng nhau nếu chúng có cùng số đo.

Nhận xét:

Nếu A là một điểm thuộc cung BAC (hình vẽ) thì:

sđ$\stackrel{⏜}{BAC}=$sđ$\stackrel{⏜}{BA}+$sđ$\stackrel{⏜}{AC}$.

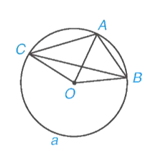
Ví dụ 3. Cho đường tròn (O) đường kính AB. Lấy điểm C thuộc (O) sao cho $\widehat{BOC}=60°$.

a) Tìm sđ$\stackrel{⏜}{BC},$sđ$\stackrel{⏜}{AC}$,sđ$\stackrel{⏜}{BAC}.$

b) Vẽ OK là phân giác của $\widehat{AOC}$(K ∈ (O)). Chứng minh rằng sđ$\stackrel{⏜}{AK}$= sđ$\stackrel{⏜}{KC}$= sđ$\stackrel{⏜}{BC}$.

c) Tính sđ$\stackrel{⏜}{BK}$.

Hướng dẫn giải

a) Vì đường tròn (O) có AB là đường kính nên sđ$\stackrel{⏜}{AB}=180°$.

Ta có:

⦁ sđ$\stackrel{⏜}{BC}=\widehat{BOC}=60°$;

⦁ sđ$\stackrel{⏜}{BAC}=360°-$sđ$\stackrel{⏜}{BC}=360°-60°=300°$;

⦁ sđ$\stackrel{⏜}{AC}=$sđ$\stackrel{⏜}{AB}-$sđ$\stackrel{⏜}{BC}=180°-60°=120°$.

Vậy sđ$\stackrel{⏜}{BC}=60°$; sđ$\stackrel{⏜}{BAC}=300°$và sđ$\stackrel{⏜}{AC}=120°$.

b) Vì sđ$\stackrel{⏜}{AC}=120°$ nên$\widehat{AOC}=120°$ .

Ta có OK là phân giác của nên:

$\widehat{AOK}=\widehat{KOC}=\frac{\widehat{AOC}}{2}=\frac{120°}{2}=60°$.

Do đó sđ$\stackrel{⏜}{AK}=$sđ$\stackrel{⏜}{KC}=60°$.

Vậy sđ$\stackrel{⏜}{AK}$= sđ$\stackrel{⏜}{KC}$= sđ$\stackrel{⏜}{BC}=60°$.

c) Ta có sđ$\stackrel{⏜}{BK}=$sđ$\stackrel{⏜}{BC}+$sđ$\stackrel{⏜}{KC}=60°+60°=120°$.

Vậy sđ$\stackrel{⏜}{BK}=120°$.

Bài tập Cung và dây của một đường tròn

Bài 1. Khẳng định nào sau đây kết luận sai?

A. Số đo của cung lớn bằng hiệu giữa 180° và số đo của cung nhỏ có chung hai mút;

B. Số đo của cung MN được kí hiệu là sđ$\stackrel{⏜}{MN}$;

C. Trong một đường tròn, đường kính là dây cung lớn nhất;

D. Số đo của nửa đường tròn bằng 180°.

Hướng dẫn giải

Đáp án đúng là: A

Phương án B, C, D đúng.

Phương án A sai. Sửa lại: Số đo của cung lớn bằng hiệu giữa 360° và số đo của cung nhỏ có chung hai mút.

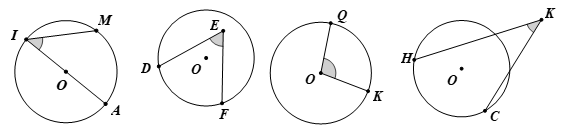
Bài 2. Cho các hình vẽ dưới đây:

Góc nào là góc ở tâm?

A. $\widehat{AIM};$

B. $\widehat{DEF};$

C. $\widehat{KOQ};$

D. $\widehat{CKH}.$

Hướng dẫn giải

Đáp án đúng là: C

$\widehat{KOQ};$ là góc ở tâm vì có đỉnh trùng với tâm của đường tròn.

Các góc $\widehat{AIM},$ $\widehat{DEF},$ $\widehat{CKH}$  không phải là góc ở tâm vì có đỉnh không trùng với tâm của đường tròn.

Bài 3. Cho AB và CD là hai dây của đường tròn (O; R). Kẻ OH, OK lần lượt vuông góc với AB và CD. Kết luận nào sau đây đúng?

A. $O{K}^2+\frac{C{D}^2}{4}>R^2$ ;

B. $O{H}^2+\frac{A{B}^2}{4}<R^2$ ;

C. $O{H}^2+\frac{A{B}^2}{4}>O{K}^2+\frac{C{D}^2}{4}$ ;

D. $O{H}^2+\frac{A{B}^2}{4}=O{K}^2+\frac{C{D}^2}{4}$ .

Hướng dẫn giải

Đáp án đúng là: D

Tam giác AOB cân tại O (vì OA = OB = R) có OH là đường cao nên OH cũng là đường trung tuyến của tam giác AOB.Do đó $HB=\frac{AB}{2}$ .

Tam giác OHB vuông tại H, theo định lí Pythagore, ta có:

OH² + HB² = OB²

Suy ra $O{H}^2+\frac{A{B}^2}{4}=R^2$ .

Chứng minh tương tự, ta được $O{K}^2+\frac{C{D}^2}{4}=R^2$ .

Từ đây ta thu được $O{H}^2+\frac{A{B}^2}{4}=O{K}^2+\frac{C{D}^2}{4}\left(=R^2\right)$ .

Vậy ta chọn phương án D.

Bài 4. Cho đường tròn (O; R). Vẽ hai dây AB và CD vuông góc với nhau tại một điểm nằm trong đường tròn. Chứng minh rằng: S_ACBD ≤ 2R².

Hướng dẫn giải

Đường tròn (O) có đường kính bằng 2R.

Ta có AB và CD là hai dây cung của đường tròn (O) nên AB < 2R và CD < 2R.

Gọi H là giao điểm của AB và CD.

Ta có $S_{ABC}=\frac{1}{2}CH\cdot AB$  và $S_{ABD}=\frac{1}{2}DH\cdot AB$ .

Suy ra $S_{ACBD}=S_{ABC}+S_{ABD}=\frac{1}{2}CH\cdot AB+\frac{1}{2}DH\cdot AB$

Do đó

$S_{ABCD}=\frac{1}{2}AB\left(CH+DH\right)=\frac{1}{2}AB\cdot CD\le \frac{1}{2}\cdot 2R\cdot 2R=2R^2$ .

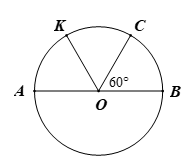
Bài 5. Cho đường tròn (O) đường kính AB, lấy điểm C nằm trên (O) sao cho $\widehat{AOC}=50°$. Vẽ dây CD vuông góc với AB (D ∈ (O)) và dây DE song song với AB (E ∈ (O)).

a) Chứng minh ba điểm C, O, E thẳng hàng.

b) Tính số đo cung nhỏ BE.

Hướng dẫn giải

a) Ta có AB ⊥ CD và DE // AB nên CD ⊥ DE hay $\widehat{CDE}=90°.$

Xét ∆OCD có OC = OD = R nên tam giác OCD cân tại O, suy ra $\widehat{OCD}=\widehat{ODC}.$

Mà $\widehat{COD}+\widehat{OCD}+\widehat{ODC}=180°$  (tổng ba góc của một tam giác)

Suy ra $\widehat{COD}=180°-2\widehat{ODC}.$

Chứng minh tương tự đối với ∆ODE ta cũng có $\widehat{DOE}=180°-2\widehat{ODE}.$

Khi đó, $\widehat{COD}+\widehat{DOE}=180°-2\widehat{ODC}+180°-2\widehat{ODE}$

Hay $\widehat{COE}=360°-2\left(\widehat{ODC}+\widehat{ODE}\right)$

                $=360°-2\cdot \widehat{CDE}=360°-2\cdot 90°=180°.$

Vậy ba điểm C, O, E thẳng hàng.

b) Vì ba điểm C, O, E thẳng hàng nên $\widehat{BOE}=\widehat{AOC}=50°.$

Do đó sđ$\stackrel{⏜}{BE}=\widehat{BOE}=50°$ .

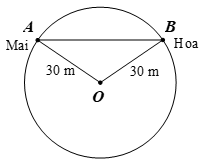
Bài 6. Trong một trò chơi, hai bạn Mai và Hoa cùng chạy trên một đường tròn tâm O có bán kính 30 m (như hình vẽ).

Có thời điểm nào dây AB nối vị trí của hai bạn đó có độ dài bằng 61 m hay không? Vì sao?

Hướng dẫn giải

Đường tròn tâm O có đường kính là: 2.30 = 60 (m).

Vì độ dài dây AB không vượt quá độ dài đường kính của đường tròn nên AB ≤ 60 (m).

Vậy không có thời điểm nào dây AB nối vị trí của hai bạn Mai và Hoa có độ dài bằng 61 m.

Học tốt Cung và dây của một đường tròn

Các bài học để học tốt Cung và dây của một đường tròn Toán lớp 9 hay khác:

• Giải sgk Toán 9 Bài 14: Cung và dây của một đường tròn