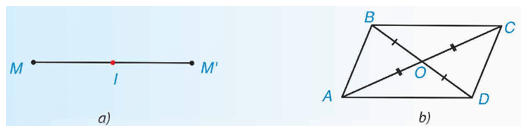Tổng hợp lý thuyết Toán 9 Chương 5 - Kết nối tri thức

---

Tổng hợp lý thuyết Toán 9 Chương 5: Đường tròn sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 9 nắm vững kiến thức trọng tâm Toán 9 Chương 5.

Tổng hợp lý thuyết Toán 9 Chương 5 - Kết nối tri thức

Lý thuyết tổng hợp Chương 5

1. Đường tròn, điểm thuộc đường tròn

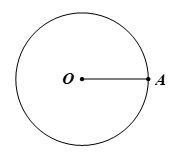
Khái niệm: Đường tròn tâm O bán kính R (R > 0), kí hiệu là (O; R), là hình gồm tất cả các điểm cách điểm O một khoảng bằng R.

⦁ Khi không cần để ý đến bán kính ta kí hiệu đường tròn tâm O là (O).

⦁ Nếu A là một điểm của đường tròn (O) thì ta viết A ∈ (O). Khi đó, ta còn nói đường tròn (O) đi qua điểm A, hay điểm A nằm trên đường tròn (O).

Nhận xét

Một cách tổng quát, ta có:

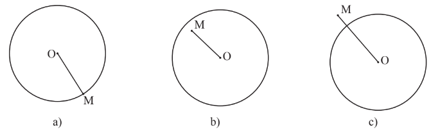
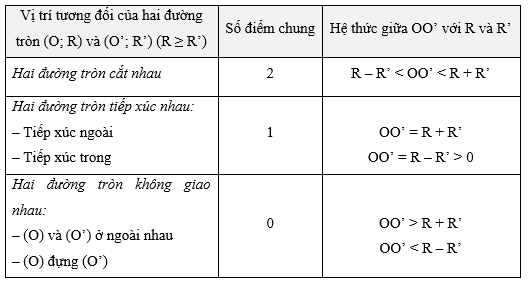
– Điểm M nằm trên đường tròn (O; R) nếu OM = R (Hình a);

– Điểm M nằm trong đường tròn (O; R) nếu OM < R (Hình b);

– Điểm M nằm ngoài đường tròn (O; R) nếu OM > R (Hình c).

Hình tròn tâm O bán kính R là hình gồm các điểm nằm trên và nằm trong đường tròn (O; R).

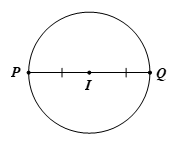
Ví dụ: Gọi I là trung điểm của PQ. Chứng minh rằng đường tròn (I; IP) đi qua Q.

Hướng dẫn giải

Vì I là trung điểm của đoạn PQ nên IP = IQ.

Do đó Q ∈ (I; IP), nói cách khác, đường tròn (I; IP) đi qua Q.

Chú ý: Ở lớp dưới, ta đã biết đoạn PQ trong Ví dụ là một đường kính của đường tròn (I). Do đó (I) còn gọi là đường tròn đường kính PQ.

2. Tính đối xứng của đường tròn

2.1.Đối xứng tâm và đối xứng trục

Đối xứng tâm

Hai điểm M và M’ gọi là đối xứng với nhau qua điểm I (hay qua tâm I) nếu I là trung điểm của đoạn thẳng MM’ (Hình a).

Chẳng hạn, nếu O là giao điểm hai đường chéo của hình bình hành ABCD thì OA = OC nên A và C đối xứng với nhau qua O. Tương tự, B và D đối xứng với nhau qua O (Hình b).

Đối xứng trục

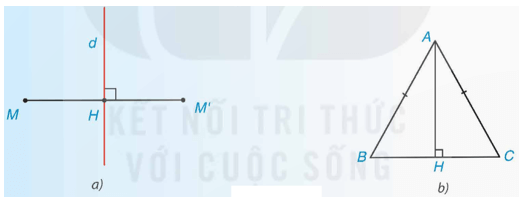
Hai điểm M và M’ gọi là đối xứng với nhau qua đường thẳng d (hay qua trục d) nếu d là đường trung trực của đoạn thẳng MM’ (Hình a).

Chẳng hạn, nếu AH là đường cao trong tam giác ABC cân tại A thì AH cũng là đường trung trực của BC, nên B và C đối xứng với nhau qua AH (Hình b).

2.2. Tâm và trục đối xứng của đường tròn

⦁ Đường tròn là hình có tâm đối xứng; tâm của đường tròn là tâm đối xứng của nó.

⦁ Đường tròn là hình có trục đối xứng; mỗi đường thẳng qua tâm của đường tròn là một trục đối xứng của nó.

Chú ý: Đường tròn có một tâm đối xứng, nhưng có vô số trục đối xứng.

3. Dây và đường kính của đường tròn

3.1. Khái niệm dây và đường kính của đường tròn

⦁ Đoạn thẳng nối hai điểm tùy ý của một đường tròn gọi là một dây (hay dây cung) của đường tròn.

⦁ Mỗi dây đi qua tâm là một đường kính của đường tròn. Dễ thấy đường kính của đường tròn bán kính R có độ dài bằng 2R.

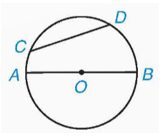
Chẳng hạn, trên hình vẽ dưới đây, CD là một dây, AB là một đường kính của (O).

3.2. Quan hệ giữa dây và đường kính

Định lí: Trong một đường tròn, đường kính là dây cung lớn nhất.

4. Góc ở tâm, cung và số đo của một cung

4.1. Khái niệm góc ở tâm và cung tròn

Cho hai điểm A và B cùng thuộc một đường tròn. Hai điểm ấy chia đường tròn thành hai phần, mỗi phần gọi là một cung tròn (hay cung). Hai điểm A và B gọi là hai mút (hay đầu mút) của mỗi cung đó.

Góc ở tâm là góc có đỉnh trùng với tâm của đường tròn.

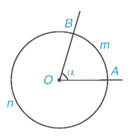
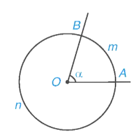
Trên hình vẽ dưới đây, ta có hai cung, kí hiệu là $\stackrel{⏜}{AmB}$và $\stackrel{⏜}{AnB}$nhưng chỉ có một góc ở tâm là $\widehat{AOB}$.

Chú ý:

⦁ Khi góc AOB không bẹt thì cung nằm trong góc AOB gọi là cung nhỏ (ở hình vẽ trên, $\stackrel{⏜}{AmB}$là cung nhỏ). Khi đó $\stackrel{⏜}{AmB}$còn có thể kí hiệu gọn là $\stackrel{⏜}{AB}$. Cung còn lại, $\stackrel{⏜}{AnB}$gọi là cung lớn. Khi góc AOB bẹt thì mỗi cung AB được gọi là một nửa đường tròn.

⦁ Ta còn nói góc AOB chắn cung AB hay cung AB bị chắn bởi góc AOB.

4.2. Cách xác định số đo của một cung

Số đo của một cung được xác định như sau:

– Số đo của nửa đường tròn bằng 180°.

– Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.

– Số đo của cung lớn bằng hiệu giữa 360° và số đo của cung nhỏ có chung hai mút.

Số đo của cung AB được kí hiệu là sđ$\stackrel{⏜}{AB}$.

Trên hình vẽ, ta có:

sđ$\stackrel{⏜}{AmB}=\widehat{AOB}=\alpha$(0° < α ≤ 180°) và sđ$\stackrel{⏜}{AnB}=360°-\alpha$.

Chú ý:

⦁ Cung có số đo n° còn gọi là cung n°. Cả đường tròn được gọi là cung 360°. Đôi khi ta cũng coi một điểm là cung 0°.

⦁ Hai cung trên một đường tròn gọi là bằng nhau nếu chúng có cùng số đo.

Nhận xét:

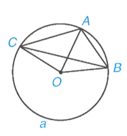
Nếu A là một điểm thuộc cung BAC (hình vẽ) thì:

sđ$\stackrel{⏜}{BAC}=$sđ$\stackrel{⏜}{BA}+$sđ$\stackrel{⏜}{AC}$.

5. Độ dài của cung tròn

⦁ Công thức tính độ dài C của đường tròn (O; R), đường kính d = 2R là:

C = πd = 2πR.        (1)

⦁ Công thức tính độ dài l của cung n° trên đường tròn (O; R) là:

$l=\frac{n}{180}\pi R$.       (2)

Nhận xét: Từ hai công thức (1) và (2), ta được $l=\frac{n}{360}\pi d=\frac{n}{360}C$ hay $\frac{l}{C}=\frac{n}{360}$, nghĩa là: Tỉ số giữa độ dài cung n° và độ dài đường tròn (cùng bán kính) đúng bằng $\frac{n}{360}$.

6. Hình quạt tròn và hình vành khuyên

6.1. Hình tròn, hình quạt tròn và hình vành khuyên

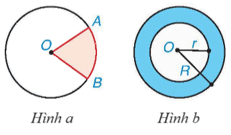
⦁Hình quạt tròn là phần hình tròn giới hạn bởi một cung tròn và hai bán kính đi qua hai đầu mút của cung đó (phần màu hồng trong Hình a).

⦁Hình vành khuyên (còn gọi là hình vành khăn) (phần màu xanh dương trong Hình b) là phần nằm giữa hai đường tròn có cùng tâm và bán kính khác nhau (còn gọi là hai đường tròn đồng tâm).

6.2. Diện tích hình quạt tròn và hình vành khuyên

⦁ Diện tích S_q của hình quạt tròn bán kính R ứng với cung n°:

$S_q=\frac{n}{360}\pi R^2=\frac{l.R}{2}$.(3)

⦁ Diện tích S_v của hình vành khuyên tạo bởi hai đường tròn đồng tâm có bán kính R và r:

S_v = π(R² – r²)(với R > r).(4)

Nhận xét: Công thức (3) có thể viết là $S_q=\frac{n}{360}S$hay $\frac{S_q}{S}=\frac{n}{360}=\frac{l}{C}$, nghĩa là:

Tỉ số giữa diện tích hình quạt tròn ứng với cung n° và diện tích hình tròn (cùng bán kính) đúng bằng $\frac{n}{360}$và bằng tỉ số giữa độ dài cung n° và độ dài đường tròn.

7. Vị trí tương đối của đường thẳng và đường tròn

Số điểm chung của đường thẳng và đường tròn

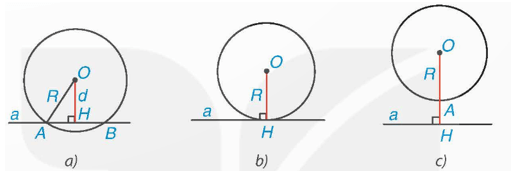
⦁Đường thẳng a và đường tròn (O) gọi là cắt nhau nếu chúng có đúng hai điểm chung (Hình a).

⦁Đường thẳng a và đường tròn (O) gọi là tiếp xúc nhau nếu chúng có duy nhất một điểm chung H. Điểm chung ấy gọi là tiếp điểm. Khi đó, đường thẳng a còn gọi là tiếp tuyến của đường tròn (O) tại H (Hình b).

⦁Đường thẳng a và đường tròn (O) gọi là không giao nhau nếu chúng không có điểm chung (Hình c).

Nhận xét:

Cho đường thẳng a và đường tròn (O; R). Gọi d là khoảng cách từ O đến a. Ta nhận thấy: Đường thẳng a và đường tròn (O; R) cắt nhau khi d < R (Hình a), tiếp xúc với nhau khi d = R (Hình b) và không giao nhau khi d > R (Hình c).

Nếu đường thẳng a tiếp xúc với đường tròn (O) tại H thì OH ⊥ a.

8. Dấu hiệu nhận biết tiếp tuyến của đường tròn

Định lí 1 (Dấu hiệu nhận biết tiếp tuyến): Nếu một đường thẳng đi qua một điểm nằm trên một đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.

9. Hai tiếp tuyến cắt nhau của một đường tròn

Định lí 2 (Tính chất hai tiếp tuyến cắt nhau):

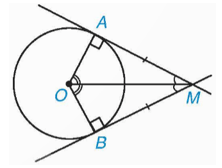
Nếu hai tiếp tuyến của đường tròn (O) cắt nhau tại điểm M thì:

⦁ Điểm M cách đều hai tiếp điểm;

⦁ MO là tia phân giác của góc tạo bởi hai tiếp tuyến;

⦁ OM là tia phân giác của góc tạo bởi hai bán kính qua hai tiếp điểm.

10. Vị trí tương đối của hai đường tròn

10.1. Hai đường tròn cắt nhau

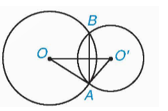
Nếu hai đường tròn có đúng hai điểm chung thì ta nói đó là hai đường tròn cắt nhau. Hai điểm chung gọi là hai giao điểm của chúng.

Nhận xét: Ta thấy hai đường tròn (O; R) và (O’; R’) cắt nhau khi:

R – R’ < OO’ < R + R’ (với R > R’).

10.2. Hai đường tròn tiếp xúc nhau

Nếu hai đường tròn có duy nhất một điểm chung thì ta nói đó là hai đường tròn tiếp xúc nhau. Điểm chung gọi là tiếp điểm của chúng.

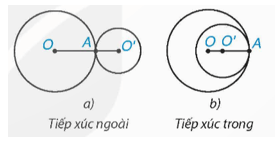
Chú ý: Người ta còn phân biệt hai trường hợp: hai đường tròn tiếp xúc ngoài (Hình a) và hai đường tròn tiếp xúc trong (Hình b).

Nhận xét:

Hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài khi OO’ = R + R’, và tiếp xúc trong khi OO’ = R – R’ (R > R’).

Nếu hai đường tròn tiếp xúc với nhau thì tiếp điểm thẳng hàng với hai tâm.

10.3. Hai đường tròn không giao nhau

Nếu hai đường tròn không có điểm chung nào thì ta nói đó là hai đường tròn không giao nhau.

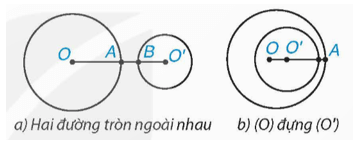
Chú ý: Người ta còn phân biệt hai trường hợp: hai đường tròn ngoài nhau (Hình a) và đường tròn này đựng đường tròn kia (Hình b).

Nhận xét:

⦁ Hai đường tròn (O; R) và (O’; R’) ngoài nhau khi OO’ > R + R’.

⦁ Đường tròn (O; R) đựng đường tròn (O’; R’) khi R > R’ và OO’ < R – R’.

Đặc biệt, khi O trùng với O’ và R ≠ R’ thì ta có hai đường tròn đồng tâm.

Ta có bảng tổng kết sau:

Bài tập ôn tập Chương 5

I. Bài tập trắc nghiệm

Bài 1. Điểm K nằm trong đường tròn (O; R) khi:

A. OK < R;

B. OK > R;

C. OK = R;

D. OK ≠ R.

Hướng dẫn giải

Đáp án đúng là: A

Điểm K nằm trong đường tròn (O; R) nếu OK < R.

Bài 2. Tâm đối xứng của đường tròn là

A. Điểm bất kì bên trong đường tròn;

B. Điểm bất kì bên ngoài đường tròn;

C. Điểm bất kì trên đường tròn;

D. Tâm của đường tròn.

Hướng dẫn giải

Đáp án đúng là: D

Tâm đối xứng của đường tròn là tâm của đường tròn.

Bài 3. Cho đường tròn (O) đường kính AB và dây CD không đi qua tâm. Khẳng định nào sau đây là đúng?

A. AB > CD;

B. AB = CD;

C. AB < CD;

D. AB ≤ CD.

Hướng dẫn giải

Đáp án đúng là: A

Trong đường tròn (O) đường kính AB thì dây AB là dây lớn nhất.

Mà dây CD không đi qua tâm nên AB > CD.

Bài 4. Cho phát biểu sau: “Nếu một đường thẳng đi qua một điểm của đường tròn và … thì đường thẳng đó là một tiếp tuyến của đường tròn”. Cụm từ thích hợp điền vào chỗ trống là

A. song song với bán kính đi qua tiếp điểm đó;

B. vuông góc với bán kính đi qua tiếp điểm đó;

C. song song với bán kính đường tròn;

D. vuông góc với bán kính bất kì.

Hướng dẫn giải

Đáp án đúng là: B

Ta có dấu hiệu nhận biết tiếp tuyến của đường tròn:

Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua tiếp điểm đó thì đường thẳng đó là một tiếp tuyến của đường tròn.

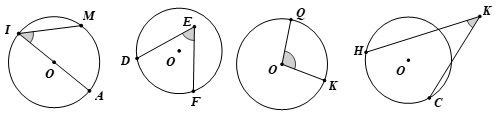
Bài5. Cho các hình vẽ dưới đây:

Góc nào là góc ở tâm?

A. $\widehat{AIM};$

B. $\widehat{DEF};$

C. $\widehat{KOQ};$

D. $\widehat{CKH}.$

Hướng dẫn giải

Đáp án đúng là: C

$\widehat{KOQ}$ là góc ở tâm vì có đỉnh trùng với tâm của đường tròn.

Các góc $\widehat{AIM},\widehat{DEF},\widehat{CKH}$  không phải là góc ở tâm vì có đỉnh không trùng với tâm của đường tròn.

Bài 6. Cho đường tròn (O) và đường thẳng d. Kẻ OH ⊥ d tại H, biết OH > R, khi đó đường thẳng d và đường tròn (O)

A. cắt nhau;

B. không cắt nhau;

C. tiếp xúc.

D. Đáp án khác.

Hướng dẫn giải

Đáp án đúng là: B

Vì OH > R nên đường thẳng d không cắt đường tròn (O).

Bài 7. Cho phát biểu sau: “Cho hai tiếp tuyến của một đường tròn cắt nhau tại một điểm. Tia nối từ điểm đó tới tâm là tia phân giác của góc tạo bởi … Tia nối từ tâm tới điểm đó là tia phân giác của góc tạo bởi …”. Hai cụm từ thích hợp điền vào chỗ trống lần lượt là

A. hai tiếp tuyến, hai bán kính đi qua tiếp điểm;

B. hai bán kính đi qua tiếp điểm, hai tiếp tuyến;

C. hai tiếp tuyến, hai dây cung;

D. hai dây cung, hai bán kính.

Hướng dẫn giải

Đáp án đúng là: A

Ta có tính chất của hai tiếp tuyến cắt nhau:

Cho hai tiếp tuyến của một đường tròn cắt nhau tại một điểm. Tia nối từ điểm đó tới tâm là tia phân giác của góc tạo bởi hai tiếp tuyến. Tia nối từ tâm tới điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua tiếp điểm.

Bài 8. Nếu hai đường tròn không cắt nhau thì số điểm chung của hai đường tròn là

A. 0;

B. 1;

C. 2;

D. 3.

Hướng dẫn giải

Đáp án đúng là: A

Nếu hai đường tròn không cắt nhau thì hai đường tròn không có điểm chung.

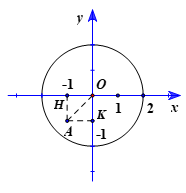
Bài 9. Trên mặt phẳng tọa độ Oxy, cho điểm A(–1; –1) và đường tròn (O; 2). Kết luận nào sau đây đúng?

A. Điểm A nằm ngoài đường tròn;

B. Điểm A nằm trên đường tròn;

C. Điểm A nằm trong đường tròn;

D. Không kết luận được.

Hướng dẫn giải

Đáp án đúng là: C

Kẻ AH ⊥ Ox tại H; AK ⊥ Oy tại K.

Khi đó OH = |x_A| = |–1| = 1; OK = |y_A| = |–1|= 1.

Tứ giác OHAK, có:  và OH = OK = 1.

Suy ra tứ giác OHAK là hình vuông, do đó AH = OH = 1.

Xét ∆OHA vuông tại H, theo định lí Pythagore ta có:

OA² = OH² + AH² = 1² + 1² = 2.

Do đó $OA=\sqrt{2}$ .

Ta có: $OA=\sqrt{2}<2$  nên điểm A nằm trong đường tròn (O; 2).

Vậy ta chọn phương án C.

Bài 10. Cung có số đo 75° của đường tròn có đường kính 12 cm dài bao nhiêu centimét?

A. 2,5 cm;

B. 2,5π cm;

C. 5π cm;

D. 5 cm.

Hướng dẫn giải

Đáp án đúng là: B

Độ dài của cung tròn đó là:

$l=\frac{n}{360}\cdot \pi d=\frac{75}{360}\cdot \pi \cdot 12=2,5\pi$ (cm).

Bài 11. Diện tích hình quạt tròn có đường kính 16 dm và độ dài cung tương ứng với nó bằng $\frac{\pi }{2}$ dm bằng

A. 2 dm²;

B. 4π dm²;

C. 2π dm²;

D. $\frac{\pi }{4}$ dm².

Hướng dẫn giải

Đáp án đúng là: C

Bán kính của hình quạt tròn đó là: $R=\frac{16}{2}=8$ (dm).

Diện tích hình quạt tròn đó là: $S_q=\frac{l.R}{2}=\frac{\frac{\pi }{2}.8}{2}=2\pi$ (dm²).

Bài 12. Diện tích hình vành khuyên được tạo bởi hai đường tròn đồng tâm có bán kính R = 6 cm và dài hơn bán kính r là 2 cm bằng

A. 20π cm²;

B. 5π cm²;

C. 10π cm²;

D. 32π cm².

Hướng dẫn giải

Đáp án đúng là: A

Bán kính r là: r = R – 2 = 6 – 2 = 4 (cm).

Diện tích hình vành khuyên cần tìm là:

S_v = π(R² – r²) = π(6² – 4²) = 20π (cm²).

II. Bài tập tự luận

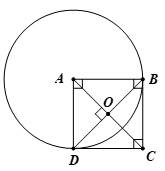
Bài 1. Cho hình vuông ABCD, O là giao điểm của hai đường chéo, $OA=2\sqrt{2}$  cm. Vẽ đường tròn (A; 4 cm). Trong các điểm O, B, C, D, xác định điểm nằm trong, nằm trên và nằm ngoài đường tròn (A; 4 cm).

Hướng dẫn giải

Hình vuông ABCD có O là giao điểm của hai đường chéo nên AC ⊥ BD, AC = BD và O là trung điểm của AC, BD.

Suy ra $OB=OA=2\sqrt{2}$  (cm) và AO ⊥ OB.

Xét ∆AOB vuông O, theo định lí Pythagore ta có:

$A{B}^2=O{A}^2+O{B}^2={\left(2\sqrt{2}\right)}^2+{\left(2\sqrt{2}\right)}^2=16.$

Do đó AB = 4 (cm).

Khi đó, AD = AB = 4 (cm) (do ABCD là hình vuông) nênhai điểm B, D nằm trên đường tròn (A; 4 cm).

Vì $OA=2\sqrt{2}$  (cm) < 4 (cm) nên điểm O nằm trong đường tròn (A; 4 cm).

Ta có $AC=2OA=2\cdot 2\sqrt{2}=4\sqrt{2}$  (cm) > 4 (cm) nên điểm C nằm ngoài đường tròn (A; 4 cm).

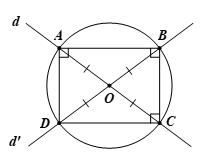
Bài 2. Cho đường tròn (O; R). Đường thẳng d đi qua tâm O, cắt đường tròn (O) tại hai điểm A, C. Đường thẳng d’ (khác d) đi qua tâm O, cắt đường tròn (O) tại hai điểm B, D. Chứng minh rằng:

a) A và C đối xứng với nhau qua điểm O; B và D đối xứng với nhau qua điểm O.

b) Tứ giác ABCD là hình chữ nhật.

Hướng dẫn giải

a) Xét đường tròn (O; R), ta có: OA = OC = R.

Suy ra O là trung điểm của AC.

Như vậy, A và C đối xứng với nhau qua điểm O.

Chứng minh tương tự, ta được B và D đối xứng với nhau qua O.

b) Ta có: AC = OA + OC = 2R và BD = OB + OD = 2R, nên AC = BD.

Xét tứ giác ABCD có O là trung điểm của AC và BD nên ABCD là hình bình hành.

Lại có AC = BD nên hình bình hành ABCD là hình chữ nhật.

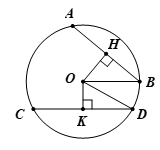
Bài 3. Cho AB và CD là hai dây của đường tròn (O; R). Kẻ OH, OK lần lượt vuông góc với AB và CD. Chứng minh rằng $O{H}^2+\frac{A{B}^2}{4}=O{K}^2+\frac{C{D}^2}{4}\left(=R^2\right).$

Hướng dẫn giải

Tam giác AOB cân tại O (vì OA = OB = R) có OH là đường cao nên OH cũng là đường trung tuyến của tam giác AOB.Do đó $HB=\frac{AB}{2}$ .

Tam giác OHB vuông tại H, theo định lí Pythagore, ta có:

OH² + HB² = OB²

Suy ra $O{H}^2+\frac{A{B}^2}{4}=R^2$ .

Chứng minh tương tự, ta được $O{K}^2+\frac{C{D}^2}{4}=R^2$ .

Từ đây ta thu được $O{H}^2+\frac{A{B}^2}{4}=O{K}^2+\frac{C{D}^2}{4}\left(=R^2\right)$ .

Bài 4. Cho đường tròn (O; R). Vẽ hai dây AB và CD vuông góc với nhau tại một điểm nằm trong đường tròn. Chứng minh rằng: S_ACBD ≤ 2R².

Hướng dẫn giải

Đường tròn (O) có đường kính bằng 2R.

Ta có AB và CD là hai dây cung của đường tròn (O) nên AB < 2R và CD < 2R.

Gọi H là giao điểm của AB và CD.

Ta có $S_{ABC}=\frac{1}{2}CH\cdot AB$  và $S_{ABD}=\frac{1}{2}DH\cdot AB$ .

Suy ra $S_{ACBD}=S_{ABC}+S_{ABD}=\frac{1}{2}CH\cdot AB+\frac{1}{2}DH\cdot AB$

Do đó

$S_{ABCD}=\frac{1}{2}AB\left(CH+DH\right)=\frac{1}{2}AB\cdot CD\le \frac{1}{2}\cdot 2R\cdot 2R=2R^2$ .

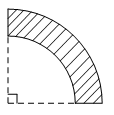
Bài 5. Hình vẽ bên dưới mô tả mặt cắt của một khúc gỗ có dạng một phần tư hình vành khuyên, trong đó hình vành khuyên giới hạn bởi hai đường tròn cùng tâm và có bán kính lần lượt là 15 cm và 20 cm. Tính diện tích mặt cắt của khúc gỗ.

Hướng dẫn giải

Diện tích mặt cắt của khúc gỗ là: $\frac{1}{4}\pi \left({20}^2-{15}^2\right)=\frac{175\pi }{4}$ (cm²).

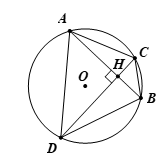
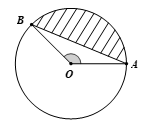
Bài 6. Cho đường tròn (O; 40 cm) có độ dài dây cung AB bằng 64 cm và $\widehat{AOB}=135°$ (hình vẽ).

Tính diện tích phần bị gạch chéo (lấy π ≈3,14).

Hướng dẫn giải

Ta có sđ$\stackrel{⏜}{AB}=\widehat{AOB}=135°$.

Diện tích hình quạt tròn bán kính R = 40 cm ứng với cung nhỏ AB có số đo bằng 135° là:

$S_q=\frac{135}{360}\pi \cdot {40}^2=600\pi \approx 600\cdot 3,14=1884$ (cm²).

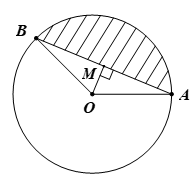
Kẻ OM ⊥ AB tại M.

Tam giác OAB cân tại O (do OA = OB = R) có OM là đường cao nên OM cũng là đường trung tuyến của tam giác OAB.

Khi đó $AM=\frac{AB}{2}=\frac{64}{2}=32$ (cm).

Tam giác OAM vuông tại M, theo định lí Pythagore, ta có: OA² = OM² + AM²

Suy ra $OM=\sqrt{O{A}^2-A{M}^2}=\sqrt{{40}^2-{32}^2}=24$  (cm).

Diện tích tam giác OAB là:

$S_{OAB}=\frac{1}{2}OM\cdot AB=\frac{1}{2}\cdot 24\cdot 64=768$ (cm²)

Diện tích phần gạch chéo là:

S = S_q – S_OAB ≈ 1 884 – 768 = 1 116 (cm²).

Bài 7. Thành phố Hồ Chí Minh nằm vào khoảng 10°24’ vĩ độ Bắc. Mỗi vòng kinh tuyến của Trái Đất dài khoảng 40 000 km. Tính độ dài cung kinh tuyến từ Thành phố Hồ Chí Minh đến xích đạo.

Hướng dẫn giải

Thành phố Hồ Chí Minh nằm vào khoảng 10°24’ vĩ độ Bắc.

Nghĩa là, kinh tuyến từ Thành phố Hồ Chí Minh đến xích đạo có số đo là 10,4°.

Độ dài cung kinh tuyến từ Thành phố Hồ Chí Minh đến xích đạo là:

$l=\frac{n}{360}C=\frac{10,4}{360}.40000=\frac{10400}{9}\approx 1155,56$ (km).

Vậy độ dài cung kinh tuyến từ Thành phố Hồ Chí Minh đến xích đạo khoảng 1155,56 km.

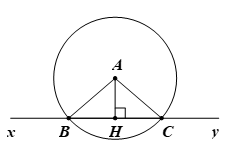
Bài 8. Cho điểm A cách đường thẳng xy một khoảng bằng 12 cm.

a) Chứng minh đường tròn (A; 13 cm) cắt đường thẳng xy tại hai điểm phân biệt.

b) Gọi hai giao điểm của (A; 13 cm) với xy là B, C. Tính độ dài đoạn thẳng BC.

Hướng dẫn giải

a) Vì điểm A cách đường thẳng xy một khoảng bằng 12 cm nên d = 12 cm.

Ta có d = 12 cm < R = 13 cm.

Vậy đường tròn (A; 13 cm) cắt đường thẳng xy tại hai điểm phân biệt.

b) Kẻ AH vuông góc với xy tại H.

Suy ra AH = d = 12 cm.

Tam giác ABH vuông tại H, theo định lí Pythagore, ta có:

AB² = AH² + BH²

Suy ra $BH=\sqrt{A{B}^2-A{H}^2}=\sqrt{{13}^2-{12}^2}=5$  (cm).

Tam giác ABC cân tại A (do AB = AC = R) có AH là đường cao nên AH cũng là đường trung tuyến của tam giác ABC.Khi đó H là trung điểm BC.

Vì vậy BC = 2BH = 2.5 = 10 (cm).

Vậy BC = 10 cm.

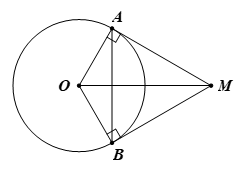
Bài 9. Cho đường tròn (O). Từ một điểm M ở ngoài (O), vẽ hai tiếp tuyến MA và MB sao cho $\widehat{AMB}=60°$. Biết chu vi tam giác AMB bằng 24 cm. Tính độ dài bán kính của đường tròn (O).

Hướng dẫn giải

Áp dụng định lí hai tiếp tuyến cắt nhau, ta có MA = MB.

Suy ra tam giác AMB cân tại M.

Mà $\widehat{AMB}=60°$nên tam giác AMB đều.

Suy ra AM = MB = AB.

Lại có chu vi tam giác AMB bằng 24 cm nên $AM=MB=AB=\frac{24}{3}=8$ (cm).

Áp dụng định lí hai tiếp tuyến cắt nhau, ta có MO là tia phân giác của $\widehat{AMB}$.

Suy ra $\widehat{AMO}=\frac{\widehat{AMB}}{2}=\frac{60°}{2}=30°$.

Vì MA là tiếp tuyến của (O) với A là tiếp điểm nên MA ⊥ OA.

Tam giác OAM vuông tại A nên:

$OA=AM\cdot \tan \widehat{AMO}=8\cdot \tan 30°=\frac{8\sqrt{3}}{3}$ (cm).

Vậy độ dài bán kính của đường tròn (O) bằng $\frac{8\sqrt{3}}{3}$ cm.

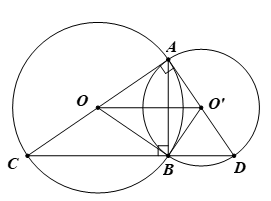
Bài10. Cho hai đường tròn (O; R) và (O’; R’) cắt nhau tại A và B. Kẻ AC, AD lần lượt là đường kính của (O) và (O’). Biết OO’ = 13 cm, R = 12 cm, R’ = 5 cm. Chứng minh rằng OA là tiếp tuyến của hai đường tròn (O), (O’) vàba điểm C, B, D thẳng hàng.

Hướng dẫn giải

⦁Ta có OA² + O’A² = R² + R’² = 12² + 5² = 169 và OO’² = 13² = 169.

Suy ra OA² + O’A² = OO’².

Áp dụng định lí Pythagore đảo, ta được tam giác OAO’ vuông tại A.

Khi đó OA ⊥ O’A tại A thuộc (O) và (O’).

Vì vậy OA là tiếp tuyến của (O) và OA cũng là tiếp tuyến của (O’).

⦁Tam giác ABC, có $OB=\frac{AC}{2}\left(=OA\right)$ và O là trung điểm AC (do AC là đường kính của (O)) hay BO là đường truyến và có độ dài bằng nửa cạnh AC.

Suy ra tam giác ABC vuông tại B, nên AB ⊥ BC.

Chứng minh tương tự, ta được AB ⊥ BD.

Vì vậy ba điểm C, B, D thẳng hàng.

Bài 11.Xác định vị trí tương đối của hai đường tròn (O; R) và (O’; R’) trong mỗi trường hợp sau:

a) OO’ = 20; R = 8; R’ = 4.

b) OO’ = 15; R = 8; R’ = 7.

c) OO’ = 6; R = 9; R’ = 4.

d) OO’ = 0; R = 7; R’ = 5.

Hướng dẫn giải

a) Ta có 20 > 8 + 4 nên OO’ > R + R’, suy ra hai đường tròn (O; R) và (O’; R’) ở ngoài nhau.

b) Ta có 15 = 8 + 7 nên OO’ = R + R’, suy ra hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài.

c) Ta có 9 – 4 < 6 < 9 + 4 nên R – R’ < OO’ < R + R’, suy ra hai đường tròn (O; R) và (O’; R’) cắt nhau.

d) Ta có 0 < 7 – 5 nên 0 = OO’ < R – R’, suy ra đường tròn (O; R) và (O’; R’) đồng tâm và đường tròn (O; R) đựng đường tròn (O’; R’).

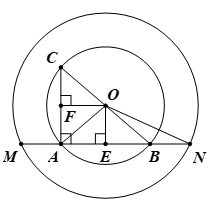
Bài 12. Cho hai đường tròn đồng tâm O, có bán kính lần lượt là R và r (R > r). Dây MN của đường tròn (O; R) cắt đường tròn (O; r) tại A và B. Gọi BC là đường kính của đường tròn (O; r). Tính giá trị của biểu thức AC² + AM² + AN² theo R và r.

Hướng dẫn giải

Kẻ OE ⊥ AB, OF ⊥ AC.

Ta có $OA=OB=OC=\frac{BC}{2}=r$

Suy ra tam giác ABC vuông tại A, nên AB ⊥ AC.

Ta có $\widehat{EAF}=\widehat{OEA}=\widehat{OFA}=90°$ nên tứ giác OEAF là hình chữ nhật.

Khi đó OF = AE và AF = OE.

Tam giác OAB cân tại O (do OA = OB) có OE là đường cao nên OE cũng là đường trung tuyến của tam giác OAB.

Do đó E là trung điểm AB hay AE = BE.

Chứng minh tương tự cho tam giác OMN, ta được E là trung điểm của MN nên ME = EN.

Suy ra ME – AE = EN – BE hay AM = BN.

Đặt AC = a, AM = b, AN = c.

Áp dụng định lí Pythagore cho tam giác OAE vuông tại E, ta được:

 $O{A}^2=O{E}^2+A{E}^2=A{F}^2+{\left(\frac{AB}{2}\right)}^2$

        $={\left(\frac{AC}{2}\right)}^2+{\left(\frac{AN-BN}{2}\right)}^2={\left(\frac{AC}{2}\right)}^2+{\left(\frac{AN-AM}{2}\right)}^2$ .

Do đó $r^2={\left(\frac{a}{2}\right)}^2+{\left(\frac{c-b}{2}\right)}^2$ .

Suy ra 4r² = a² + (c – b)²

Hay (2r)² = a² + c² + b² – 2bc      (1)

Áp dụng định lí Pythagore cho tam giác OEN vuông tại E, ta được:

$O{N}^2=O{E}^2+E{N}^2=A{F}^2+{\left(\frac{MN}{2}\right)}^2={\left(\frac{AC}{2}\right)}^2+{\left(\frac{AM+AN}{2}\right)}^2$.

Do đó $R^2={\left(\frac{a}{2}\right)}^2+{\left(\frac{b+c}{2}\right)}^2$ .

Suy ra 4R² = a² + (b + c)².

Hay (2R)² = a² + b² + c² + 2bc       (2)

Lấy (1) cộng (2) vế theo vế, ta được:

2(a² + b² + c²) = (2R)² + (2r)²

Suy ra $a^2+b^2+c^2=\frac{4\left(R^2+r^2\right)}{2}$

Hay AC² + AM² + AN² = 2(R² + r²).

Vậy AC² + AM² + AN² = 2(R² + r²).

Học tốt Toán 9 Chương 5

Các bài học để học tốt Bài tập cuối chương 5 Toán lớp 9 hay khác:

• Giải sgk Toán 9 Bài tập cuối chương 5