Lý thuyết Toán 9 Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên - Kết nối tri thức

---

Haylamdo biên soạn tóm tắt lý thuyết Toán 9 Bài 15: Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên sách Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh lớp 9 nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 9.

Lý thuyết Toán 9 Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên - Kết nối tri thức

Lý thuyết Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên

1. Độ dài của cung tròn

⦁ Công thức tính độ dài C của đường tròn (O; R), đường kính d = 2R là:

C = πd = 2πR.        (1)

⦁ Công thức tính độ dài l của cung n° trên đường tròn (O; R) là:

$l=\frac{n}{180}\pi R$.       (2)

Nhận xét: Từ hai công thức (1) và (2), ta được $l=\frac{n}{360}\pi d=\frac{n}{360}C$ hay $\frac{l}{C}=\frac{n}{360}$, nghĩa là: Tỉ số giữa độ dài cung n° và độ dài đường tròn (cùng bán kính) đúng bằng $\frac{n}{360}$.

Ví dụ 1.

a) Cung có số đo 150° của đường tròn bán kính 5 m dài bao nhiêu mét?

b) Cung có số đo 45° của đường tròn có chu vi 18π cm dài bao nhiêu centimét?

Hướng dẫn giải

a) Độ dài của cung tròn đó là:

$l=\frac{n}{180}\pi R=\frac{150}{180}\pi \cdot 5=\frac{25\pi }{6}$ (m).

b) Độ dài của cung tròn đó là:

$l=\frac{n}{360}\cdot C=\frac{45}{360}\cdot 18\pi =\frac{9\pi }{4}$ (cm).

2. Hình quạt tròn và hình vành khuyên

2.1. Hình tròn, hình quạt tròn và hình vành khuyên

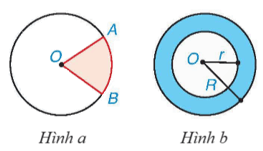
⦁Hình quạt tròn là phần hình tròn giới hạn bởi một cung tròn và hai bán kính đi qua hai đầu mút của cung đó (phần màu hồng trong Hình a).

⦁Hình vành khuyên (còn gọi là hình vành khăn) (phần màu xanh dương trong Hình b) là phần nằm giữa hai đường tròn có cùng tâm và bán kính khác nhau (còn gọi là hai đường tròn đồng tâm).

Ví dụ 2.

– Một số ví dụ về hình quạt tròn trong thực tế:

– Một số ví dụ về hình vành khuyên trong thực tế:

2.2. Diện tích hình quạt tròn và hình vành khuyên

⦁ Diện tích S_q của hình quạt tròn bán kính R ứng với cung n°:

$S_q=\frac{n}{360}\pi R^2=\frac{l.R}{2}$.          (3)

⦁ Diện tích S_v của hình vành khuyên tạo bởi hai đường tròn đồng tâm có bán kính R và r:

S_v = π(R² – r²)  (với R > r).        (4)

Nhận xét: Công thức (3) có thể viết là $S_q=\frac{n}{360}S$hay $\frac{S_q}{S}=\frac{n}{360}=\frac{l}{C}$, nghĩa là:

Tỉ số giữa diện tích hình quạt tròn ứng với cung n° và diện tích hình tròn (cùng bán kính) đúng bằng $\frac{n}{360}$ và bằng tỉ số giữa độ dài cung n° và độ dài đường tròn.

Ví dụ 3.

a) Tính diện tích hình quạt tròn bán kính 4 cm ứng với cung 30°.

b) Tính diện tích hình vành khuyên nằm giữa hai đường tròn đồng tâm có bán kính lần lượt là 7 cm và 9 cm.

Hướng dẫn giải

a) Diện tích hình quạt tròn cần tìm là:

$S_q=\frac{n}{360}\pi R^2=\frac{30}{360}\pi \cdot 4^2=\frac{4\pi }{3}$(cm²).

b) Diện tích hình vành khuyên cần tìm là:

S_v = π.(9² – 7²) = 32π (cm²).

Bài tập Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên

Bài 1. Cung có số đo 75° của đường tròn có đường kính 12 cm dài bao nhiêu centimét?

A. 2,5 cm;

B. 2,5π cm;

C. 5π cm;

D. 5 cm.

Hướng dẫn giải

Đáp án đúng là: B

Độ dài của cung tròn đó là:

$l=\frac{n}{360}\cdot \pi d=\frac{75}{360}\cdot \pi \cdot 12=2,5\pi$ (cm).

Bài 2. Diện tích hình quạt tròn có đường kính 16 dm và độ dài cung tương ứng với nó bằng $\frac{\pi }{2}$ dm bằng

A. 2 dm²;

B. 4π dm²;

C. 2π dm²;

D. $\frac{\pi }{4}$ dm².

Hướng dẫn giải

Đáp án đúng là: C

Bán kính của hình quạt tròn đó là: $R=\frac{16}{2}=8$ (dm).

Diện tích hình quạt tròn đó là: $S_q=\frac{l.R}{2}=\frac{\frac{\pi }{2}.8}{2}=2\pi$ (dm²).

Bài 3. Diện tích hình vành khuyên được tạo bởi hai đường tròn đồng tâm có bán kính R = 6 cm và dài hơn bán kính r là 2 cm bằng

A. 20π cm²;

B. 5π cm²;

C. 10π cm²;

D. 32π cm².

Hướng dẫn giải

Đáp án đúng là: A

Bán kính r là: r = R – 2 = 6 – 2 = 4 (cm).

Diện tích hình vành khuyên cần tìm là:

S_v = π(R² – r²) = π(6² – 4²) = 20π (cm²).

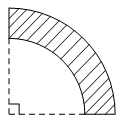
Bài 4. Hình vẽ bên dưới mô tả mặt cắt của một khúc gỗ có dạng một phần tư hình vành khuyên, trong đó hình vành khuyên giới hạn bởi hai đường tròn cùng tâm và có bán kính lần lượt là 15 cm và 20 cm. Tính diện tích mặt cắt của khúc gỗ.

Hướng dẫn giải

Diện tích mặt cắt của khúc gỗ là: $\frac{1}{4}\pi \left({20}^2-{15}^2\right)=\frac{175\pi }{4}$ (cm²).

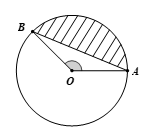
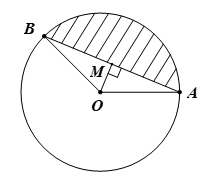
Bài 5. Cho đường tròn (O; 40 cm) có độ dài dây cung AB bằng 64 cm và $\widehat{AOB}=135°$ (hình vẽ).

Tính diện tích phần bị gạch chéo (lấy π ≈3,14).

Hướng dẫn giải

Ta có sđ$\stackrel{⏜}{AB}=\widehat{AOB}=135°$.

Diện tích hình quạt tròn bán kính R = 40 cm ứng với cung nhỏ AB có số đo bằng 135° là:

$S_q=\frac{135}{360}\pi \cdot {40}^2=600\pi \approx 600\cdot 3,14=1884$ (cm²).

Kẻ OM ⊥ AB tại M.

Tam giác OAB cân tại O (do OA = OB = R) có OM là đường cao nên OM cũng là đường trung tuyến của tam giác OAB.

Khi đó $AM=\frac{AB}{2}=\frac{64}{2}=32$ (cm).

Tam giác OAM vuông tại M, theo định lí Pythagore, ta có: OA² = OM² + AM²

Suy ra $OM=\sqrt{O{A}^2-A{M}^2}=\sqrt{{40}^2-{32}^2}=24$  (cm).

Diện tích tam giác OAB là:

$S_{OAB}=\frac{1}{2}OM\cdot AB=\frac{1}{2}\cdot 24\cdot 64=768$ (cm²)

Diện tích phần gạch chéo là:

S = S_q – S_OAB ≈ 1 884 – 768 = 1 116 (cm²).

Bài 6. Thành phố Hồ Chí Minh nằm vào khoảng 10°24’ vĩ độ Bắc. Mỗi vòng kinh tuyến của Trái Đất dài khoảng 40 000 km. Tính độ dài cung kinh tuyến từ Thành phố Hồ Chí Minh đến xích đạo.

Hướng dẫn giải

Thành phố Hồ Chí Minh nằm vào khoảng 10°24’ vĩ độ Bắc.

Nghĩa là, kinh tuyến từ Thành phố Hồ Chí Minh đến xích đạo có số đo là 10,4°.

Độ dài cung kinh tuyến từ Thành phố Hồ Chí Minh đến xích đạo là:

$l=\frac{n}{360}C=\frac{10,4}{360}.40000=\frac{10400}{9}\approx 1155,56$ (km).

Vậy độ dài cung kinh tuyến từ Thành phố Hồ Chí Minh đến xích đạo khoảng 1155,56 km.

Học tốt Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên

Các bài học để học tốt Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên Toán lớp 9 hay khác:

• Giải sgk Toán 9 Bài 15: Độ dài của cung tròn. Diện tích hình quạt tròn và hình vành khuyên