Các bài toán liên quan đến mệnh đề phủ định và cách giải - Toán lớp 10

---

Các bài toán liên quan đến mệnh đề phủ định và cách giải

Với Các bài toán liên quan đến mệnh đề phủ định và cách giải Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập bài toán liên quan đến mệnh đề phủ định từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

1. Lý thuyết:

Cho mệnh đề P.

- Mệnh đề “ không phải P ” được gọi là mệnh đề phủ định của P và kí hiệu là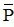

- Nếu P đúng thì 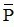sai, nếu P sai thì 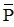đúng.

2. Phương pháp giải:

- Phủ định của mệnh đề P là mệnh đề “ không phải P”.

- Phủ định của quan hệ = là quan hệ ≠ và ngược lại.

- Phủ định của quan hệ > là quan hệ ≤ và ngược lại.

- Phủ định của quan hệ < là quan hệ ≥ và ngược lại.

- Phủ định liên kết “và” là liên kết “hoặc” và ngược lại.

- Mệnh đề phủ định của “ ∀x ∈ X; P(x) ” là: “∃x ∈ X; ”.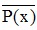

- Mệnh đề phủ định của “∃x ∈ X;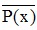” là “ ∀x ∈ X; P(x) ”.

3. Ví dụ minh họa:

Ví dụ 1: Phát biểu mệnh đề phủ định của các mệnh đề sau:

a. P: “ Mọi hình thoi là hình vuông”.

b. P: “ Số chính phương có thể có chữ số tận cùng là 0; 1; 4; 5; 6; 9 ”.

c. P: “ Đường thẳng đi qua một điểm và vuông góc với đường thẳng cho trước là duy nhất”.

Hướng dẫn:

a. 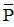: “ Tồn tại hình thoi không là hình vuông”.

b. 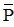: “ Số chính phương không thể có chữ số tận cùng là 0; 1; 4; 5; 6; 9 ”.

c. 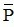: “ Đường thẳng đi qua một điểm và vuông góc với đường thẳng cho trước không là duy nhất”.

Ví dụ 2: Xét xem các mệnh đề sau đúng hay sai, lập mệnh đề phủ định của mệnh đề:

a. ∀x ∈ R, x² - x + 1 > 0.

b. ∃x ∈ N, (n + 2)(n + 1) = 0.

c. ∃x ∈ Q, x² = 3.

Hướng dẫn:

a. Mệnh đề đúng, vì x² - x + 1 = 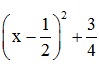> 0, ∀x.

Mệnh đề phủ định là ∃x ∈ R, x² - x + 1 ≤ 0.

b. Mệnh đề sai, vì (n + 2)(n + 1) = 0 ⇒ n = -2 hoặc n = -1 đều không thuộc N .

Mệnh đề phủ định là ∀n ∈ N, (n + 2)(n + 1) ≠ 0 .

c. Mệnh đề sai, vì x² = 3 ⇒ x = ±√3 ∉ Q.

Mệnh đề phủ định là ∀x ∈ Q, x² ≠ 3 .

Ví dụ 3: Nêu mệnh đề phủ định của mệnh đề: “∀n ∈ N, n² + 1 không chia hết cho 3”.

Hướng dẫn:

Phủ định của ∀ là ∃. Phủ định của “không chia hết” là “chia hết”.

Mệnh đề phủ định của mệnh đề “∀n ∈ N, n² + 1 không chia hết cho 3” là:

“ ∃n ∈ N, n² + 1 chia hết cho 3”.

4. Bài tập tự luyện:

Câu 1: Chọn khẳng định sai:

A. Cho mệnh đề P và mệnh đề phủ định 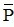, nếu P đúng thì 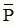sai và điều ngược lại chắc đúng.

B. Mệnh đề P và mệnh đề phủ định 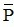cùng đúng hoặc cùng sai.

C. Mệnh đề phủ định của mệnh đề P là mệnh đề “ không phải P” được kí hiệu là .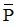

D. Mệnh đề P: “ π là số hữu tỷ” khi đó mệnh đề phủ định 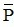là: “ π là số vô tỷ”.

Hướng dẫn:

Chọn B. Theo lý thuyết nếu P đúng thì 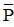sai và ngược lại

Câu 2: Phủ định của mệnh đề: “ Có ít nhất một số vô tỷ là số thập phân vô hạn tuần hoàn” là mệnh đề nào sau đây:

A. Mọi số vô tỷ đều là số thập phân vô hạn tuần hoàn.

B. Có ít nhất một số vô tỷ là số thập phân vô hạn không tuần hoàn.

C. Mọi số vô tỷ đều là số thập phân vô hạn không tuần hoàn.

D. Mọi số vô tỷ đều là số thập phân tuần hoàn.

Hướng dẫn:

Chọn C.

Phủ định của “có ít nhất” là “mọi”.

Phủ định của “tuần hoàn” là “không tuần hoàn”.

Vậy mệnh đề phủ định của mệnh đề đã cho là: “Mọi số vô tỷ đều là số thập phân vô hạn không tuần hoàn”.

Câu 3: Cho mệnh đề A “ ∀x ∈ R, x² - x + 7 < 0”. Mệnh đề phủ định 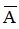của mệnh đề A là:

A. ∀x ∈ R, x² - x + 7 > 0 .

B. ∀x ∈ R, x² - x + 7 ≥ 0 .

C. Không tồn tại x : x - x + 7 < 0 .

D. ∃x ∈ R, x² - x + 7 ≥ 0 .

Hướng dẫn:

Chọn D.

Theo lý thuyết, mệnh đề phủ định của “∀x ∈ X; P(x)” là: “∃x ∈ X; ”.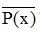

Vậy mệnh đề phủ định 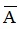của mệnh đề A là: ∃x ∈ R, x² - x + 7 ≥ 0 .

Câu 4: Mệnh đề phủ định của mệnh đề P “ ∃x : x² + 2x + 5 là số nguyên tố” là :

A. ∀x : x² + 2x + 5 không là số nguyên tố.

B. ∃x : x² + 2x + 5 là hợp số.

C. ∀x : x² + 2x + 5 là hợp số.

D. ∃x : x² + 2x + 5 là số thực.

Hướng dẫn :

Chọn A.

Phủ định của ∃ là ∀ .

Phủ định của “ là số nguyên tố” là “ không là số nguyên tố”.

Vậy mệnh đề phủ định 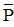của mệnh đề P là : ∀x : x² + 2x + 5 không là số nguyên tố.

Câu 5: Mệnh đề nào sau đây là phủ định của mệnh đề: “ Mọi phương trình đều có nghiệm”

A. Mọi phương trình đều vô nghiệm.

B. Tất cả các phương trình đều không có nghiệm.

C. Có ít nhất một phương trình vô nghiệm.

D. Có duy nhất một phương trình vô nghiệm.

Hướng dẫn:

Chọn C.

Phủ định của “mọi” là “có ít nhất”.

Phủ định của “vô nghiệm” là “có nghiệm”.

Vậy mệnh đề phủ định của mệnh đề đã cho là: Có ít nhất một phương trình vô nghiệm.

Câu 6: Mệnh đề phủ định của mệnh đề P: “∃x ∈ R, 5x - 3x² = 1” là:

A. ∃x ∈ R, 5x - 3x².

B. ∀x ∈ R, 5x - 3x² = 1.

C. ∀x ∈ R, 5x - 3x² ≠ 1.

D. ∃x ∈ R, 5x - 3x² ≥ 1.

Hướng dẫn:

Chọn C.

Phủ định của ∃ là ∀ .

Phủ định của = là ≠ .

Vậy mệnh đề phủ định 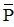của mệnh đề P là : ∀x ∈ R, 5x - 3x² ≠ 1.

Câu 7: Cho mệnh đề P(x): " ∀x ∈ R, x² + x + 1 > 0". Mệnh đề phủ định của mệnh đề P(x) là:

A. ∀x ∈ R, x² + x + 1 < 0 .

B. ∀x ∈ R, x² + x + 1 ≤ 0 .

C. ∃x ∈ R, x² + x + 1 ≤ 0 .

D. 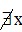∈ R, x² + x + 1 > 0 .

Hướng dẫn:

Chọn C.

Phủ định của ∀ là ∃ .

Phủ định của > là ≤ .

Vậy mệnh đề phủ định của mệnh đề P(x) là: ∃x ∈ R, x³ + x +1 ≤ 0 .

Câu 8: Trong các mệnh đề sau, mệnh đề nào đúng?

A. Phủ định của mệnh đề “∀x ∈ R, 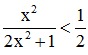” là mệnh đề “∀x ∈ R, ”.

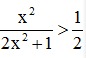B. Phủ định của mệnh đề “∀k ∈ Z, k² + k + 1 là một số lẻ” là mệnh đề “∀k ∈ Z, k² + k + 1 là một số chẵn”.

C. Phủ định của mệnh đề “∀n ∈ N sao cho n² - 1 chia hết cho 24” là mệnh đề “ ∀n ∈ N sao cho n² - 1 không chia hết cho 24”.

D. Phủ định của mệnh đề “∀x ∈ Q, x³ - 3x + 1 > 0” là mệnh đề “∀x ∈ Q, x³ - 3x + 1 ≤ 0”.

Hướng dẫn:

Chọn B: vì phủ định của ∀ là ∃, phủ định của số lẻ là số chẵn.

Đáp án A sai vì phủ định của < phải là ≥.

Đáp án C sai vì phủ định của ∀ phải là ∃ .

Đáp án D sai vì phủ định của ∀ phải là ∃.

Câu 9: Mệnh đề phủ định của mệnh đề “ Có ít nhất một số thực x thỏa mãn điều kiện bình phương của nó là 1 số không dương” là:

A. ∀x ∈ : x² > 0.

B. ∃x ∈ R : x² ≤ 0.

C. ∀x ∈ R : x² ≤ 0.

D. ∃x ∈ R : x² > 0.

Hướng dẫn:

Chọn A.

Theo giả thiết, ta có mệnh đề P: "∃x ∈ R : x² ≤ 0" .

Vậy mệnh đề phủ định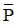của mệnh đề P là: ∀x ∈ R : x² > 0.

Câu 10: Cho mệnh đề “ Phương trình x² - 4x + 4 = 0 có nghiệm”. Mệnh đề phủ định của mệnh đề đã cho và tính đúng, sai của mệnh đề phủ định là:

A. Phương trình x² - 4x + 4 = 0 có nghiệm. Đây là mệnh đề đúng.

B. Phương trình x² - 4x + 4 = 0 có nghiệm. Đây là mệnh đề sai.

C. Phương trình x² - 4x + 4 = 0 vô nghiệm. Đây là mệnh đề đúng.

D. Phương trình x² - 4x + 4 = 0 vô nghiệm. Đây là mệnh đề sai.

Hướng dẫn :

Chọn D.

Phủ định của “có nghiệm” là “vô nghiệm”.

Vậy mệnh đề phủ định của mệnh đề đã cho là: Phương trình x² - 4x + 4 = 0 vô nghiệm.

Mệnh đề phủ định sai do phương trình x² - 4x + 4 = 0 có nghiệm là 2.