Các bài toán về các tập hợp số và cách giải - Toán lớp 10
Các bài toán về các tập hợp số và cách giải
Với Các bài toán về các tập hợp số và cách giải Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Các bài toán về các tập hợp số từ đó đạt điểm cao trong bài thi môn Toán lớp 10.
1. Lý thuyết:
- Tập hợp con của R : N ⊂ Z ⊂ Q ⊂ R Trong đó:
N : là tập hợp số tự nhiên.
Z : là tập hợp số nguyên.
Q : là tập hợp số hữu tỷ.
R = ( -∞; +∞): là tập hợp số thực.
- Các tập hợp con thường dùng của R
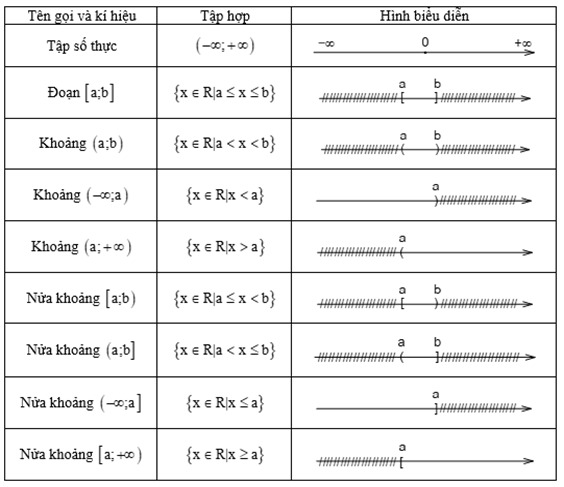
2. Phương pháp giải:
Sử dụng trục số, đoạn (hoặc khoảng) nào không lấy, ta gạch bỏ, sử dụng tính chất giao và hợp của các tập hợp để tìm ra kết quả.
3. Ví dụ minh họa:
Ví dụ 1: Xác định mỗi tập hợp sau và biểu diễn nó trên trục số.
a. (-3;3) ∪ ( -1;0) .
b. (-1;3) ∪ [0;5] .
c. (-2;2] ∩ [1;3) .
Hướng dẫn:
Sử dụng trục số, đoạn (hoặc khoảng) nào không lấy, ta gạch bỏ, sử dụng tính chất giao và hợp của các tập hợp để tìm ra kết quả.
a. (-3;3) ∪ ( -1;0) = (-3; 3).
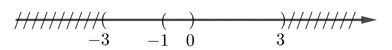
b. (-1;3) ∪ [0;5] = (-1; 5].
c. (-2;2] ∩ [1;3) = [1; 2]
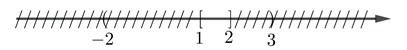
Ví dụ 2: Cho các tập hợp :
A = {x ∈ R | -3 ≤ x ≤ 2} .
B = {x ∈ R | 0 < x ≤ 7}.
C = {x ∈ R | x ≤ -1} .
D = {x ∈ R | x ≥ 5}.
Hãy dùng kí hiệu đoạn, khoảng, nửa khoảng để viết lại các tập hợp trên.
Hướng dẫn:
- Theo lý thuyết:[a;b] = {x ∈ R | a ≤ x ≤ b} .
Vậy A = {x ∈ R | -3 ≤ x ≤ 2} = [-3; 2].
- Theo lý thuyết: (a; b] = {x ∈ R | a < x ≤ b} .
Vậy B = {x ∈ R | 0 < x ≤ 7} = (0; 7].
- Theo lý thuyết: (-∞; 1) = { x ∈ R | x < b } .
Vậy C = {x ∈ R | x < -1} = (-∞; 1).
- Theo lý thuyết: [a; +∞) = {x ∈ R | a ≤ x} .
Vậy D = {x ∈ R | x ≥ 5} = [5; +∞).
Ví dụ 3: Cho hai tập hợp A = {x ∈ R | -5 ≤ x < 1}; B = {x ∈ R | -3 < x ≤ 3}. Tìm A ∩ B
Hướng dẫn:
Ta có: A = {x ∈ R | -5 ≤ x < 1} = [-5; 1) ( theo lý thuyết: [a; b) = {x ∈ R | -3 ≤ x < b} )
B = {x ∈ R | -3 < x ≤ 3} = (-3; 3] ( theo lý thuyết: (a; b] = {x ∈ R | a < x ≤ b})
Ta biểu diễn tập hợp A và B trên trục số như sau:
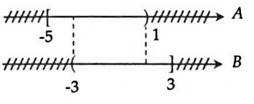
Vậy A ∩ B = (-3; 1).
4. Bài tập tự luyện:
Câu 1: Cho tập hợp A = {x ∈ R | -3 < x < 1} . Tập A là tập nào sau đây?
A.{-3; 1}.
B. [-3; 1].
C. [-3; 1).
D. (-3; 1).
Hướng dẫn:
Chọn D.
Theo lý thuyết: (a;b) = {x ∈ R | a < x < b}
Vậy A = {x ∈ R | -3 < x < 1} = (-3; 1).
Câu 2: Hình vẽ nào sau đây (phần không bị gạch) minh họa cho tập hợp (1; 4]?
A. 
B.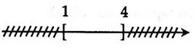 
C. 
D. 
Hướng dẫn:
Chọn A. Vì (1; 4] gồm các số thực x mà 1 < x ≤ 4 .
Đáp án B sai vì [1; 4] gồm các số thực x mà 1 ≤ x ≤ 4 .
Đáp án C sai vì (1; 4) gồm các số thực x mà 1 < x < 4.
Đáp án B sai vì [1; 4) gồm các số thực x mà 1 ≤ x ≤ 4.
Câu 3: Sử dụng các kí hiệu khoảng, đoạn để viết tập hợp A = { x ∈ R | 4 ≤ x ≤ 9} :
A. A = [4; 9].
B. A = (4; 9].
C. A = [4; 9).
D. A = (4; 9)
Hướng dẫn:
Chọn A.
Theo lý thuyết: [a;b] = {x ∈ R | a ≤ x ≤ b} . Suy ra A = {x ∈ R | 4 ≤ x ≤ 9} = [4; 9] .
Câu 4: Cho hai tập hợp A = [-2; 7); B = (1; 9]. Tìm A ∪ B.
A. (1; 7).
B. [-2; 9].
C. [-2; 1).
D. (7; 9].
Hướng dẫn:
Chọn B.
Ta biểu diễn tập hợp A và B trên trục số như sau:
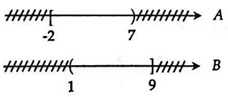
Vậy A ∪ B = [-2;7] ∪ (1;9] = [-2;9] .
Câu 5: Cho tập hợp X = thì X được biểu diễn là hình nào sau đây?
A.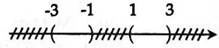 
B. 
C. 
D. 
Hướng dẫn:
Chọn D.
Giải bất phương trình:
1 ≤ |x| ≤ 3 ⇔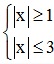 
⇔ 
⇔ 
⇔ 
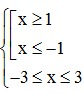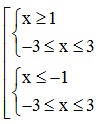
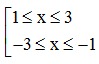⇔ x ∈ [-3;-1] ∪ [1;3].
Vậy đáp án D thỏa mãn x ∈ [-3;-1] ∪ [1;3] .
Câu 6: Cho hai tập hợp A = (1; 5]; B = (2; 7]. Tập hợp A \ B là:
A. (1; 2].
B. (2; 5).
C. (-1; 7].
D. (-1; 2).
Hướng dẫn:
Chọn A.
Ta biểu diễn tập hợp A và B trên trục số:
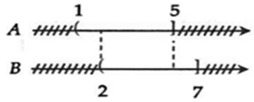
Vậy A \ B = { x ∈ R | x ∈ A và x ∉ B } ⇒ x ∈ (1; 2] .
Câu 7: Cho các số thực a, b, c, d và a < b < c < d. Khẳng định nào sau đây là đúng?
A. (a; c) ∩ (b; d) = (b; c)
B. (a; c) ∩ (b; d) = (b; c]
C. (a; c) ∩ (b; d) = [b; c)
D. (a; c) ∪ (b; d) = [b; c)
Hướng dẫn:
Chọn A.
Ta biểu diễn (a; c); (b; d) trên trục số sau đó dựa vào tính chất giao của hai tập hợp để tìm ra đáp án:
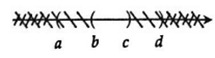
Vậy (a; c) ∩ (b; d) = (b; c).
Câu 8: Cho tập hợp A = [m; m+2]; B = [-1; 2]. Tìm điều kiện của m để A ⊂ B.
A. m ≤ -1 hoặc m ≥ 0 .
B. -1 ≤ m ≤ 0 .
C. -1 ≤ m ≤ 2 .
D. m < 1 hoặc m > 2.
Hướng dẫn:
Chọn B.
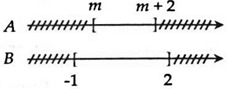
Điều kiện để A ⊂ B là: -1 ≤ m < m + 2 ≤ 2 ⇔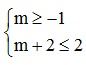 
⇔ 
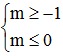⇔ -1 ≤ m ≤ 0 .
Câu 9: Cho hai tập hợp A = [-2; 3]; B = (m; m+6). Điều kiện để A ⊂ B là:
A. -3 ≤ m ≤ -2
B. -3 < m < -2
C. m < -3
D. m ≥ -2
Hướng dẫn:
Chọn B.
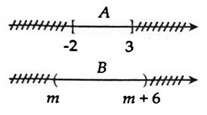
Điều kiện để A ⊂ B là m < -2 < 3 < m + 6 ⇔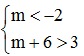 
⇔ 
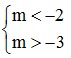⇔ -3 < m < 2 .
Câu 10: Cho hai tập hợp X = (0; 3] và Y = (a; 4). Tìm tất cả các giá trị của a ≤ 4 để X ∩ Y ≠ ∅ .
A.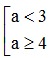 
.
B. a < 3.
C. a < 0.
D. a > 3.
Hướng dẫn:
Chọn B.
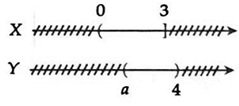
Xét: X ∩ Y ≠ ∅ ⇔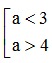 
⇔ 3 ≤ a ≤ 4
⇒ X ∩ Y ≠ ∅ ⇔ 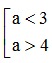. Mà theo đề bài, a ≤ 4 nên suy ra a < 3.
Vậy với a < 3 thì X ∩ Y ≠ ∅ .
