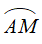Lý thuyết Cung và góc lượng giác hay, chi tiết - Toán lớp 10

---

Lý thuyết Cung và góc lượng giác hay, chi tiết

Tài liệu Lý thuyết Cung và góc lượng giác hay, chi tiết Toán lớp 10 sẽ tóm tắt kiến thức trọng tâm về Cung và góc lượng giác từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 10.

I. KHÁI NIỆM CUNG VÀ GÓC LƯỢNG GIÁC

1. Đường tròn định hướng và cung lượng giác

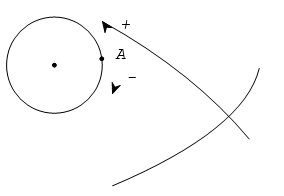
Đường tròn định hướng là một đường tròn trên đó ta chọn một chiều chuyển động gọi là chiều dương, chiều ngược lại là chiều âm. Ta quy ước chọn chiều ngược với chiều quay của kim đồng hồ làm chiều dương.

Trên đường tròn định hướng cho hai điểm A và B. Một điểm M di động trên đường tròn luôn theo một chiều (âm hoặc dương) từ A đến B tạo nên một cung lượng giác có điểm đầu A điểm cuối B.

Với hai điểm A, B đã cho trên đường tròn định hướng ta có vô số cung lượng giác điểm đầu A, điểm cuối B. Mỗi cung như vậy đều được kí hiệu là

2. Góc lượng giác

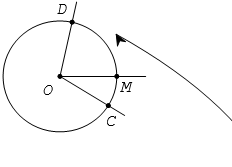
Trên đường tròn định hướng cho một cung lượng giác Một điểm M chuyển động trên đường tròn từ C tới D tạo nên cung lượng giác nói trên. Khi đó tia OM quay xung quanh gốc O từ vị trí OC tới vị trí OD. Ta nói tia OM tạo ra một góc lượng giác, có tia đầu là OC, tia cuối là OD.

Kí hiệu góc lượng giác đó là (OC, OD).

3. Đường tròn lượng giác

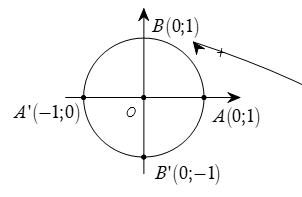
Trong mặt phẳng tọa độ Oxy, vẽ đường tròn định hướng tâm O bán kính R = 1.

Đường tròn này cắt hai trục tọa độ tại bốn điểm

A(1; 0), A’(–1; 0); B(0; 1); B(0; –1).

Ta lấy A(1; 0) làm điểm gốc của đường tròn đó.

Đường tròn xác định như trên được gọi là đường tròn lượng giác (gốc A).

II. SỐ ĐO CỦA CUNG VÀ GÓC LƯỢNG GIÁC

1. Độ và radian

a) Đơn vị radian

Trên đường tròn tùy ý, cung có độ dài bằng bán kính được gọi là cung có số đo 1 rad.

b) Quan hệ giữa độ và radian

c) Độ dài của một cung tròn

Trên đường tròn bán kính R, cung nửa đường tròn có số đo là π rad và có độ dài là πR. Vậy cung có số đo α rad của đường tròn bán kính R có độ dài

l = Rα.

2. Số đo của một cung lượng giác

Số đo của một cung lượng giác 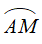(A ≠ M) là một số thực âm hay dương.

Kí hiệu số đo của cung 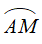là sđ .

Ghi nhớ

Số đo của các cung lượng giác có cùng điểm đầu và điểm cuối sai khác nhau một bội của 2π.

Ta viết

sđ 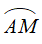= α + k2π , k ∈ Z

trong đó α là số đo của một cung lượng giác tùy ý có điểm đầu là A, điểm cuối là M

3. Số đo của một góc lượng giác

Số đo của góc lượng giác (OA, OC) là số đo của cung lượng giác 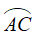tương ứng.

Chú ý Vì mỗi cung lượng giác ứng với một góc lượng giác và ngược lại, đồng thời số đo của các cung và góc lượng giác tương ứng là trùng nhau, nên từ nay về sau khi ta nói về cung thì điều đó cũng đúng cho góc và ngược lại.

4. Biểu diễn cung lượng giác trên đường tròn lượng giác

Chọn điểm gốc A(1; 0) làm điểm đầu của tất cả các cung lượng giác trên đường tròn lượng giác. Để biểu diễn cung lượng giác có số đo α trên đường tròn lượng giác ta cần chọn điểm cuối M của cung này. Điểm cuối M được xác định bởi hệ thức sđ = α