Lý thuyết Giá trị lượng giác của một cung hay, chi tiết - Toán lớp 10

---

Lý thuyết Giá trị lượng giác của một cung hay, chi tiết

Tài liệu Lý thuyết Giá trị lượng giác của một cung hay, chi tiết Toán lớp 10 sẽ tóm tắt kiến thức trọng tâm về Giá trị lượng giác của một cung từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 10.

I. GIÁ TRỊ LƯỢNG GIÁC CỦA CUNG α

1. Định nghĩa

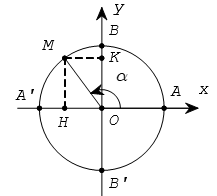
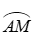
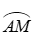
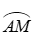
Trên đường tròn lượng giác cho cung có sđ = α (còn viết = α)

Tung độ y = 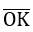của điểm M gọi là sin của α và kí hiệu là sinα

sin α =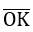

Hoành độ x = 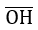của điểm M gọi là côsin của α và kí hiệu là cosα

cos α =

Nếu cos α ≠ 0, tỉ số 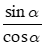gọi là tang của α và kí hiệu là tan α (người ta còn dùng kí hiệu tg α)

Tan α =

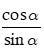
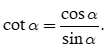
Nếu sinα ≠ 0 tỉ số gọi là côtang của α và kí hiệu là cotα (người ta còn dùng kí hiệu cotg α)

Các giá trị sinα, cosα, tanα, cotα được gọi là các giá trị lượng giác của cung α. Ta cũng gọi trục tung là trục sin, còn trục hoành là trục côsin

2. Hệ quả

1) sinα và cosα xác định với mọi α ∈ R. Hơn nữa, ta có

sin(α + k2π) = sin α, ∀k ∈ Z;

cos(α + k2π) = cos α, ∀k ∈ Z

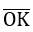
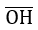
2) Vì –1 ≤ ≤ 1; –1 ≤ ≤ 1 nên ta có

–1 ≤ sin α ≤ 1

–1 ≤ cos α ≤ 1

3) Với mọi m ∈ R mà –1 ≤ m ≤ 1 đều tồn tại α và β sao cho sin α = m và cos β = m.

4) tanα xác định với mọi α ≠ 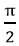+ kπ (k ∈ Z)

5) cotα xác định với mọi α ≠ kπ (k ∈ Z)

6) Dấu của các giá trị lượng giác của góc α phụ thuộc vào vị trí điểm cuối của cung = α trên đường tròn lượng giác.

Bảng xác định dấu của các giá trị lượng giác

Giá trị lượng giác |Góc phần tư	I	II	III	IV
cos α	+	-	-	+
sin α	+	+	-	-
tan α	+	-	+	-
cot α	+	-	+	-

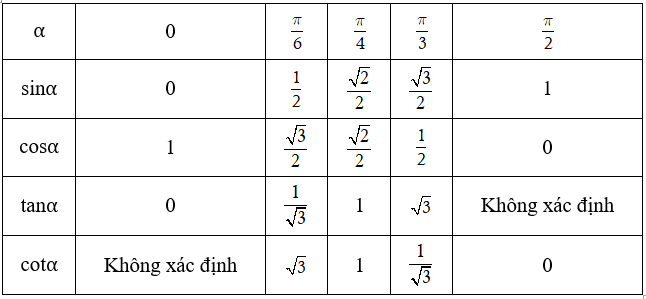
3. Giá trị lượng giác của các cung đặc biệt

II. Ý NGHĨA HÌNH HỌC CỦA TANG VÀ CÔTANG

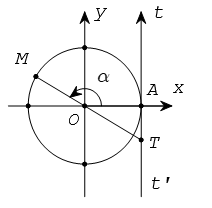
1. Ý nghĩa hình học của tan α

Từ A vẽ tiếp tuyến t’At với đường tròn lượng giác. Ta coi tiếp tuyến này là một trục số bằng cách chọn gốc tại A.

Gọi T là giao điểm của OM với trục t’At.

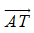
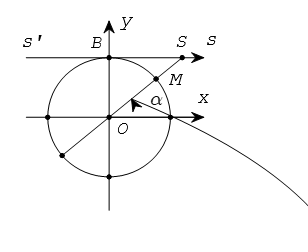
tanα được biểu diễn bởi độ dài đại số của vectơ trên trục t’At. Trục t’At được gọi là trục tang.

2. Ý nghĩa hình học của cot α

Từ B vẽ tiếp tuyến s’Bs với đường tròn lượng giác. Ta coi tiếp tuyến này là một trục số bằng cách chọn gốc tại B.

Gọi S là giao điểm của OM với trục s’Bs

cot α được biểu diển bởi độ dài đại số của vectơ 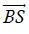trên trục s’Bs. Trục s’Bs được gọi là trục côtang.

III – QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC

1. Công thức lượng giác cơ bản

Đối với các giá trị lượng giác, ta có các hằng đẳng thức sau

sin²α + cos²α = 1

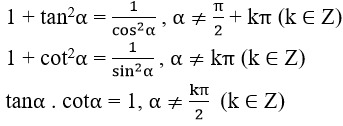
2. Giá trị lượng giác của các cung có liên quan đặc biệt

1) Cung đối nhau: α và –α

cos(-α) = cosα

sin(-α) = –sinα

tan(-α) = –tanα

cot(-α) = –cotα

2) Cung bù nhau: α và π-α

sin(π-α) = sinα

cos(π-α) = –cosα

tan(π-α) = –tanα

cot(π-α) = –cotα

3) Cung hơn kém π : α và (α + π)

sin(α + π) = –sinα

cos(α + π) = –cosα

tan(α + π) = tanα

cot(α + π) = cotα

4) Cung phụ nhau: α và ( 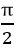– α)

sin(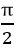 – α) = cos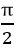α

cos( – α) = sinα

tan(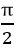 – α) = cotα

cot( – α) = tanα