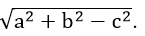Lý thuyết Phương trình đường tròn hay, chi tiết - Toán lớp 10
Lý thuyết Phương trình đường tròn hay, chi tiết
Tài liệu Lý thuyết Phương trình đường tròn hay, chi tiết Toán lớp 10 sẽ tóm tắt kiến thức trọng tâm về Phương trình đường tròn từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 10.
1. Phương trình đường tròn có tâm và bán kính cho trước
Trong mặt phẳng Oxy, đường tròn (C ) tâm I(a; b) bán kính R có phương trình:
(x – a)2 + (y – b)2 = R2
Chú ý. Phương trình đường tròn có tâm là gốc tọa độ O và bán kính R là x2 + y2 = R2
2. Nhận xét
+) Phương trình đường tròn (x – a)2 + (y – b)2 = R2 có thể viết dưới dạng
x2 + y2 – 2ax – 2by + c = 0
trong đó c = a2 + b2 – R2.
+) Phương trình x2 + y2 – 2ax – 2by + c = 0 là phương trình của đường tròn (C) khi a2 + b2 – c2 > 0. Khi đó, đường tròn (C) có tâm I(a; b), bán kính R = 
3. Phương trình tiếp tuyến của đường tròn
Cho đường tròn (C) có tâm I(a; b) và bán kính R.
Đường thẳng Δ là tiếp tuyến với (C) tại điểm Mo(xo; yo).
Ta có
+) Mo(xo; yo) thuộc Δ.
+)
= (x0 – a; y0 – b) là vectơ pháp tuyến của Δ.
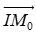
Do đó Δ có phương trình là
(xo – a).(x – xo) + (yo – b).(y – yo) = 0.
