Lý thuyết Phương trình và hệ phương trình bậc nhất nhiều ẩn hay, chi tiết - Toán lớp 10

Lý thuyết Phương trình và hệ phương trình bậc nhất nhiều ẩn hay, chi tiết

Tài liệu Lý thuyết Phương trình và hệ phương trình bậc nhất nhiều ẩn hay, chi tiết Toán lớp 10 sẽ tóm tắt kiến thức trọng tâm về Phương trình và hệ phương trình bậc nhất nhiều ẩn từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 10.

I. ÔN TẬP VỀ PHƯƠNG TRÌNH VÀ HỆ HAI PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

1. Phương trình bậc nhất hai ẩn

Phương trình bậc nhất hai ẩn x , y có dạng tổng quát là

ax + by = c (1)

trong đó a, b, c là các hệ số, với điều kiện a và b không đồng thời bằng 0.

CHÚ Ý

a) Khi a = b = 0 ta có phương trình 0x + 0y = c. Nếu c ≠ 0 thì phương trình này vô nghiệm, còn nếu c = 0 thì mọi cặp số (x_o; y_o) đều là nghiệm.

b) Khi b ≠ 0, phương trình ax + by = c trở thành

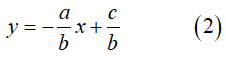
Cặp số (x_o; y_o) là một nghiệm của phương trình (1) khi và chỉ khi điểmM(x_o; y_o) thuộc đường thẳng (2).

Tổng quát, người ta chứng minh được rằng phương trình bậc nhất hai ẩn luôn luôn có vô số nghiệm. Biểu diễn hình học tập nghiệm của phương trình của phương trình (1) là một đường thẳng trong mặt phẳng tọa độ Oxy.

2. Hệ hai phương trình bậc nhất hai ẩn

Hệ phương trình bậc nhất hai ẩn có dạng tổng quát là

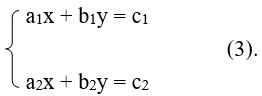
Trong đó x, y là hai ẩn; các chữ số còn lại là hệ số.

Nếu cặp số (x0; y0) đồng thời là nghiệm của cả hai phương trình của hệ thì (x0; y0) được gọi là một nghiệm của hệ phương trình (3).

Giải hệ phương trình (3) là tìm tập nghiệm của nó.

II. HỆ BA PHƯƠNG TRÌNH BẬC NHẤT BA ẨN

Phương trình bậc nhất ba ẩn có dạng tổng quát là

ax + by + cz = d,

trong đó x, y, z là ba ẩn a, b, c, d là các hệ số và a, b, c không đồng thời bằng 0.

Hệ phương trình bậc nhất ba ẩn có dạng tổng quát là

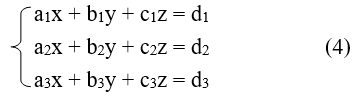
Trong đó x, y, z là ba ẩn; các chữ còn lại là các hệ số.

Mỗi bộ ba số (x_o; y_o; z_o) nghiệm đúng ba phương trình của hệ được gọi là một nghiệm của hệ phương trình (4).