Cách xác định Hàm số bậc hai hay, chi tiết - Toán lớp 10
Cách xác định Hàm số bậc hai hay, chi tiết
Với Cách xác định Hàm số bậc hai hay, chi tiết Toán lớp 10 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập xác định Hàm số bậc hai từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

1. Phương pháp giải.
Để xác định hàm số bậc hai ta là như sau
Gọi hàm số cần tìm là y = ax2 + bx + c, a ≠ 0. Căn cứ theo giả thiết bài toán để thiết lập và giải hệ phương trình với ẩn a, b, c từ đó suy ra hàm số cần tìm.
2. Các ví dụ minh họa.
Ví dụ 1. Xác định parabol (P) : y = ax2 + bx + c, a ≠ 0, biết:
a) (P) đi qua A (2; 3) và có đỉnh I (1; 2)
b) c = 2 và (P) đi qua B (3; -4) và có trục đối xứng là x = (-3)/2.
c) Hàm số y = ax2 + bx + c có giá trị nhỏ nhất bằng 3/4 khi x = 1/2 và nhận giá trị bằng 1 khi x = 1.
d) (P) đi qua M (4; 3) cắt Ox tại N (3; 0) và P sao cho ΔINP có diện tích bằng 1 biết hoành độ điểm P nhỏ hơn 3. (I là đỉnh của (P)).
Hướng dẫn:
a) Vì A ∈ (P) nên 3 = 4a + 2b + c
Mặt khác (P) có đỉnh I(1;2) nên:
(-b)/(2a) = 1 ⇔ 2a + b = 0
Lại có I ∈ (P) suy ra a + b + c = 2
Ta có hệ phương trình:
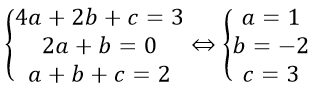
Vậy (P) cần tìm là y = x2 - 2x + 3.
b) Ta có c = 2 và (P) đi qua B(3; -4) nên -4 = 9a + 3b + 2 ⇔ 3a + b = -2
(P) có trục đối xứng là x = (-3)/2 nên (-b)/(2a) = -3/2 ⇔ b = 3a
Ta có hệ phương trình:
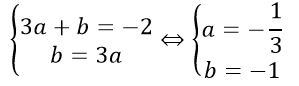

Vậy (P) cần tìm là y = (-1)x2/3 - x + 2.
c) Hàm số y = ax2 + bx + c có giá trị nhỏ nhất bằng 3/4 khi x = 1/2 nên ta có:
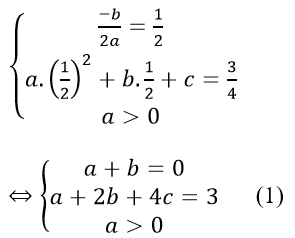
Hàm số y = ax2 + bx + c nhận giá trị bằng 1 khi x = 1 nên a + b + c = 1 (2)
Từ (1) và (2) ta có hệ phương trình:
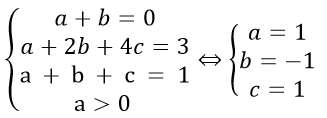
Vậy (P) cần tìm là y = x2 - x + 1.
d) Vì (P) đi qua M (4; 3) nên 3 = 16a + 4b + c (1)
Mặt khác (P) cắt Ox tại N (3; 0) suy ra 0 = 9a + 3b + c (2)
Từ (1) và (2) ta có: 7a + b = 3 ⇒ b = 3 - 7a
(P) cắt Ox tại P nên P (t; 0) (t < 3) ⇒ NP = 3 - t
Theo định lý Viét ta có

Ta có:
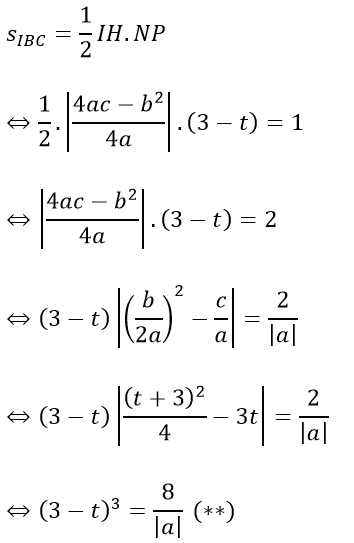
Thay (*) vào (**) ta được:
(3 - t)3 = 8(4-t)/3 ⇔ 3t3 - 27t2 + 73t - 49 = 0 ⇔ t = 1
Suy ra a = 1; b = - 4; c = 3.
Vậy (P) cần tìm là y = x2 - 4x + 3.

