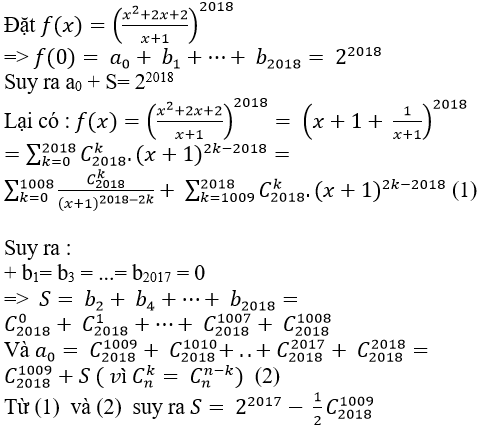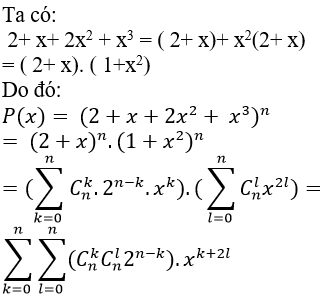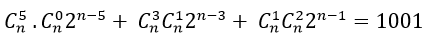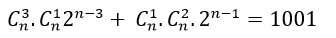Bài tập về nhị thức Newton nâng cao cực hay có lời giải - Toán lớp 11

---

Bài tập về nhị thức Newton nâng cao cực hay có lời giải

Với Bài tập về nhị thức Newton nâng cao cực hay có lời giải Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập nhị thức Newton từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Ví dụ minh họa

Ví dụ 1: Gọi Tk là số hạng thứ k trong khai triển (x³+2y²)¹³ mà tổng số mũ của x và y trong số hạng đó bằng 32. Hệ số của T_k bằng?

A.198620    B.186284    C.219648    D.2012864

Hướng dẫn giải :

Đáp án : C

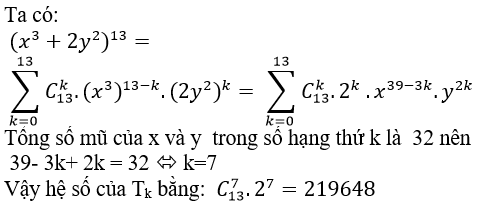
Ví dụ 2: Cho khai triển: (x-1)²ⁿ+x.(x+1)^(2n-1)= a₀+ a₁ x+ a₂.x²+⋯+ a_2n.x²ⁿ với n nguyên dương và n≥3. Biết rằng 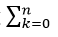a_2k=768. Tính a₆

A.188     B.284     C.336    D.424

Hướng dẫn giải :

Đáp án : C

Đặt P(x)= (x-1)²ⁿ+x.(x+1)^(2n-1)= a₀+ a₁ x+ a₂.x²+⋯+ a_2n.x²ⁿ

⇒ P(1)= 2^{2n- 1} =a₀+ a₁ + ...+ a_2n

Và P(-1)= 2²ⁿ = a₀- a₁ + a₂- ....+ a_2n

⇒ P(1) + P(-1) = 2^2n-1 +2²ⁿ = 2. 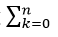a_2k=768= 1536

Suy ra: 2^2n-1 +2²ⁿ = 1536 ⇔ n= 5

⇒hệ số a6 chứa x6 trong khai triển đã cho là:

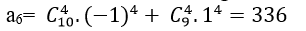
Ví dụ 3: Gọi S là tổng các hệ số của các lũy thừa bậc nguyên dương của x trong khai triển nhị thức: P(x) = (x+ 1/x)²⁰¹⁸. Tính S + 1/2 C¹⁰⁰⁹₂₀₁₈

Hướng dẫn giải :

Đáp án : B

Ví dụ 4: Tìm n,biết rằng hệ số của x⁴ trong khai triển (x³+2x²+3x).(x+1)ⁿ bằng 804

A.n=10    B.n=11     C.n=12    D.n=13

Hướng dẫn giải :

Đáp án : C

Ví dụ 5: Cho khai triển an (x-1)ⁿ + a_n-1(x-1)^n-1 + ...+ a₁(x-1)+ a₀ = xⁿ vớ mọi số thực x; n∈N; n> 4. Tìm n biết a₂+ a₃+ a₄ = 83n

A.n=10    B.n=11    C.n=12    D.n=13

Hướng dẫn giải :

Đáp án : D

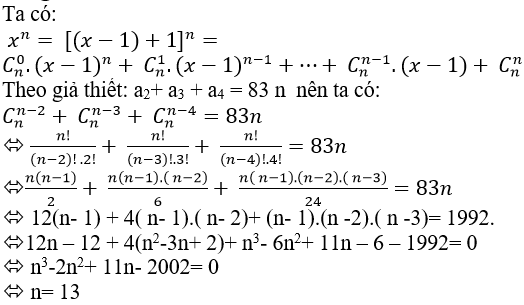
Ví dụ 6: Sau khi khai triển và rút gọn biểu thức (x - 1/x²)²⁰+ (x³- 1/x)¹⁰ có tất cả bao nhiêu số hạng?

A.29     B.28     C.27    D.26

Hướng dẫn giải :

Đáp án : A

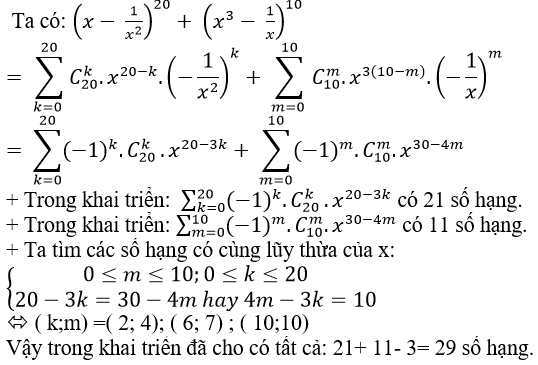
Ví dụ 7: Có bao nhiêu số thực x để khi khai triển nhị thức (2^x+ 2^(1/2-x))ⁿ có tổng số hạng thứ 3 và thứ 5 bằng 135; còn tổng của ba số hạng cuối là 22.

A.1    B.2    C.3    D.4

Hướng dẫn giải :

Đáp án : B

Ví dụ 8: Trong khai triển của biểu thức (x³-x-2)²⁰¹⁷. Tính tổng S của các hệ số của x^{2k+ 1} với k nguyên dương.

A.2017.2²⁰¹⁷    B.2017.2²⁰¹⁶     C.2016.2²⁰¹⁶    D.2018.2²⁰¹⁷

Hướng dẫn giải :

Đáp án : B

B. Bài tập trắc nghiệm

Câu 1: Gọi a_{3n- 3} là hệ số của số hạng chứa x^{3n- 3} trong khai triển (x₂+1)ⁿ.(x+2)ⁿ. Tìm n sao cho a_{3n- 3} = 26n?

A.n=4    B.n=5    C.n=6    D.n=7

Lời giải:

Đáp án : B

Câu 2: Gọi a_5n-10 là hệ số của số hạng chứa x^5n-10 tronh khai triển (x³+1)ⁿ.(x²+2)ⁿ. Biết a_{5n- 10} = 1000n( n-1). Tìm n

A.n=13    B.n=15    C.n=16    D.n=17

Lời giải:

Đáp án : D

Ta có

Câu 3: Cho kahi triển x(x+1)ⁿ + 2( x+1)ⁿ= a₀+ a₁x+ a₂.x²+ ...+ a_n+1xⁿ⁺¹ với n là số tự nhiên và n≥2. Tìm n; biết rằng a₂ – 7n; n.a_n ; a_n-2 theo thứ tự đó lập thành một cấp số cộng.

A.n= 6    B.n= 8    C.n= 10    D.n= 12

Lời giải:

Đáp án : C

Ta có

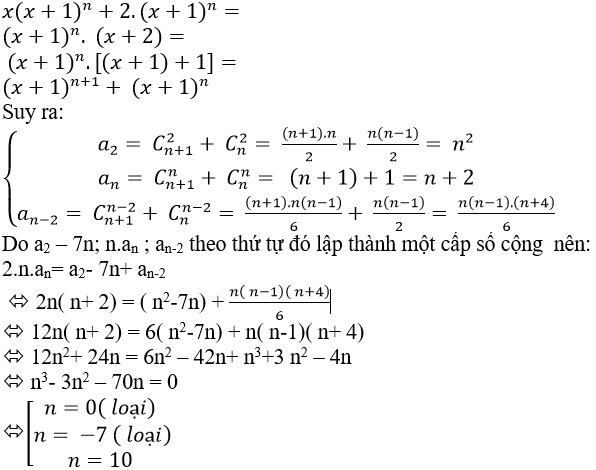
Vậy n=10

Câu 4: Xác định n biết rằng hệ số của xn trong khai triển (1+x+2x²+⋯+n.xⁿ )² bằng 6n

A.n= 5    B.n= 6    C.n= 4    D.n= 7

Lời giải:

Đáp án : A

Ta có

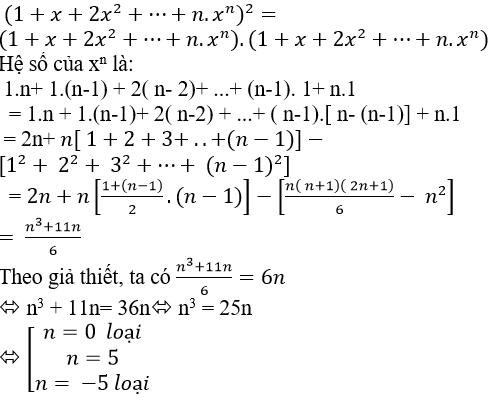
Vậy n=10

Câu 5: Khai triển (1+x+ x²+ ..+ x¹⁰)¹¹ được viết thành a₀+ a₁x+ a₂.x²+ ...+a₁₁₀x¹¹⁰.

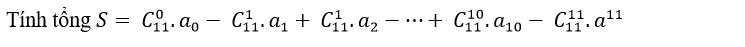
A.S= 9     B.S= 10    C.S= 13     D.S= 11

Lời giải:

Đáp án : D

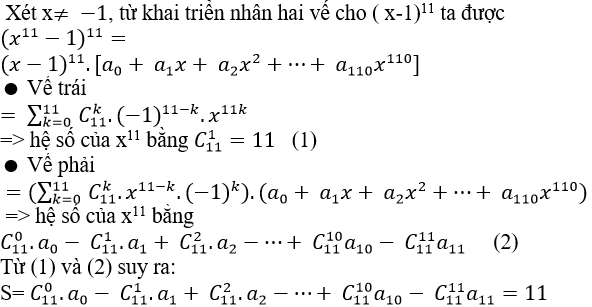
Câu 6: Biết rằng trong khai triển nhị thức Niu- tơn của đa thức P(x)= (2+x+ 2x²+ x³)ⁿ thì hệ số của x⁵ là 1001. Tổng các hệ số trong khai triển của P(x) bằng :

A.7776     B.6784    C.6842    D.8640

Lời giải:

Đáp án : A

Hệ số của x⁵ ứng với k+ 2l thỏa mãn : k+ 2l= 5

⇒ (k; l)= { (5; 0); (3,1); (1;2)}

Trường hợp 1. Với n≥5 khi đó (k; l)= { (5; 0); (3,1); (1;2)}

⇒ Hệ số của x⁵ là :

Vì vế trái lẻ mà vế phải luôn chẵn nếu n>5 do đó chỉ có thể chọn n=5.

Thử lại vào phương trình ta thấy thỏa mãn điều kiện.

Trường hợp 2. Với 3≤n<5 khi đó (k; l) = {(3;1); (1;2)}

⇒ Hệ số của x⁵ là :

Vì vế trái lẻ mà vế phải luôn chẵn nếu n>3 do đó chỉ có thể chọn n= 3

Thử lại vào phương trình ta thấy n= 3 không thỏa mãn điều kiện.

Trường hợp 3. Với n= 2 khi đó (k;l)= (1;2)

⇒ Hệ số của x⁵ là :

Do đó chỉ có n= 5 thỏa mãn nên tổng các hệ số trong khai triển:

Cho x= 1 ta được: 65 = 7776

Câu 7: Cho khai triển P(x)= (1+x).(2+ x). ..(1+2017x) = a₀+ a₁x+ a₂x²+ ...+ a₂₀₁₇x²⁰¹⁷. Kí hiệu P’(x) và P”(x) lần lượt là đạo hàm cấp 1 và đạo hàm cấp 2 của đa thức P(x). Khẳng định nào sau đây đúng?

A.a₂ = P’(0)     B.a₂=(P'(0))/2     C.a₂=P''(0)    D.a₂=(P^''(0))/2

Lời giải:

Đáp án : D

Ta có: P'(x)= a₁+2a₂x+3a₃x²+⋯+2017a₂₀₁₇x²⁰¹⁶

Tiếp tục đạo hàm lần nữa, ta có:

P''(x)=2a₂+6a₃x+⋯+2017.2016.a₂₀₁₇x²⁰¹⁵

Cho x = 0 ta được: P''(0)=2a₂ nên a₂=(P^''(0))/2

Câu 8: Tìm hệ số của số hạng chứa x³ trong khai triển: (1-2x+2015x²⁰¹⁶-2016x²⁰¹⁷+2017.x²⁰¹⁸)⁶⁰

Lời giải:

Đáp án : A

Câu 9: Cho khai triển

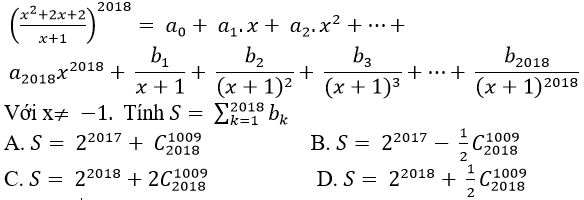
Lời giải:

Đáp án : B