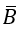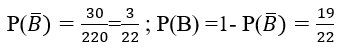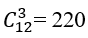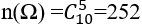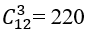60 bài tập trắc nghiệm Xác suất chọn lọc, có lời giải - Toán lớp 11

---

60 bài tập trắc nghiệm Xác suất chọn lọc, có lời giải

Với 60 bài tập trắc nghiệm Xác suất chọn lọc, có lời giải Toán lớp 11 tổng hợp 60 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Xác suất từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

Bài 1: Một hộp chứa 7 bi xanh, 5 bi đỏ, 3 bi vàng. Xác suất để trong lần thứ nhất bốc được một bi mà không phải là bi đỏ là:

A. 1/3.        B. 2/3.        C. 10/21.        D. 11/21.

Lời giải:

Đáp án: B

Chọn B.

+ Số phần tử của không gian mẫu là : n(Ω)=15

+ Gọi biến cố A " lần thứ nhất bốc được một bi mà không phải bi đỏ "

Ta có : n(A)=10

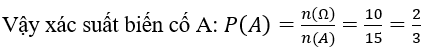
Bài 2: Một chứa 6 bi đỏ, 7 bi xanh. Nếu chọn ngẫu nhiên 5 bi từ hộp này. Thì xác suất đúng đến phần trăm để có đúng 2 bi đỏ là:

A. 0,14.        B. 0,41        C. 0,28.        D. 0,34.

Lời giải:

Đáp án: B

Chọn B.

Bài 3: Một hộp chứa 6 bi xanh, 7 bi đỏ. Nếu chọn ngẫu nhiên 2 bi từ hộp này. Thì xác suất để được 2 bi cùng màu là:

A. 0,46.        B. 0,51.        C. 0,55.        D. 0,64.

Lời giải:

Đáp án: A

Chọn A.

+ Số phần tử của không gian mẫu là : n(Ω)=6

+ Gọi biến cố A " hai viên bi được chọn cùng màu"

Ta có : n(A)=13

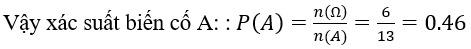
Bài 4: Một hộp chứa 3 bi xanh, 2 bi đỏ, 4 bi vàng. Lấy ngẫu nhiên 3 bi. Xác suất để đúng một bi đỏ là:

A. 1/3.        B. 2/5.        C. 1/2.        D. 3/5.

Lời giải:

Đáp án: C

Chọn C.

Bài 5: Có 3 chiếc hộp. Hộp A chứa 3 bi đỏ, 5 bi trắng. Hộp B chứa 2 bi đỏ, hai bi vàng. Hộp C chứa 2 bi đỏ, 3 bi xanh. Lấy ngẫu nhiên một hộp rồi lấy một bi từ hộp đó. Xác suất để được một bi đỏ là:

A. 1/8.        B. 1/6.        C. 2/15.        D. 17/40.

Lời giải:

Đáp án: D

Chọn D.

Lấy ngẫu nhiên một hộp

Gọi C₁ là biến cố lấy được hộp A

Gọi C₂ là biến cố lấy được hộp B

Gọi C₃ là biến cố lấy được hộp C

Vậy P(C₁ )=P(C₂ )=P(C₃ )=1/3

Gọi C là biến cố " lấy ngẫu nhiên một hộp, trong hộp đó lại lấy ngẫu nhiên một viên bi và được bi đỏ " là C=(C ∩ C₁ ) ∪ (C ∩ C₂ ) ∪ (C ∩ C₃ )

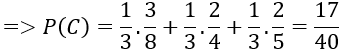
Bài 6: Cho phép thử có không gian mẫu Ω={1,2,3,4,5,6}. Các cặp biến cố không đối nhau là:

A. A={1} và B={2,3,4,5,6}        B. A={1,4,5} và B={2,3,6}

C. A={1,4,6} và B={2,3}        D. Ω

Lời giải:

Đáp án: C

Chọn C.

Cặp biến cố không đối nhau là E={1,4,6} và F={2,3}

Bài 7: Một hộp đựng 10 thẻ, đánh số từ đến 10. Chọn ngẫu nhiên 3 thẻ. Gọi A là biến cố để tổng số của thẻ được chọn không vượt quá 8. Số phần tử của biến cố A là:

A. 2.        B.3.        C.4.        D. 5.

Lời giải:

Đáp án: C

Chọn C.

Liệt kê ta có: A={(1,2,3);(1,2,4);(1,2,5);(1,3,4)}

Bài 8: Xét phép thử tung con súc sắc 6 mặt hai lần. Xác định số phần tử của không gian mẫu

A. 36        B. 40        C. 38        D. 35

Lời giải:

Đáp án: A

Chọn A.

Không gian mẫu gồm các bộ (i,j), trong đó i,j ∈ {1,2,3,4,5,6}

i nhận 6 giá trị,j cũng nhận 6 giá trị nên có 6.6=36 bộ

Vậy. n(Ω)=36

Bài 9: Cho A là một biến cố liên quan phép thử T. Mệnh đề nào sau đây là mệnh đề đúng ?

Lời giải:

Đáp án: B

Chọn B

Loại trừ :A ;B ;C đều sai

Bài 10: Gieo đồng tiền hai lần. Xác suất để sau hai lần gieo thì mặt sấp xuất hiện ít nhất một lần

A. 1/4.        B. 1/2.        C. 3/4.        D. 1/3.

Lời giải:

Đáp án: C

Chọn C.

Số phần tử không gian mẫu: n(Ω)=2.2=4

Biến cố xuất hiện mặt sấp ít nhất một lần: A={SN,NS,SS}

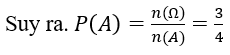
Bài 11: Gieo đồng tiền lần cân đối và đồng chất. Xác suất để được ít nhất một lần xuất hiện mặt sấp là:

A. 31/32.        B. 21/32.        C. 11/32.        D. 1/32.

Lời giải:

Đáp án: A

Chọn A.

Phép thử : Gieo đồng tiền 5 lần cân đối và đồng chất

Ta có n(Ω)=2⁵

Biến cố A : Được ít nhất một lần xuất hiện mặt sấp

B: Tất cả đều là mặt ngửa

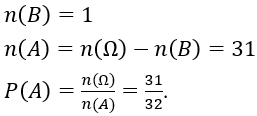
Bài 12: Một lớp có 20 học sinh nam và 18 học sinh nữ. Chọn ngẫu nhiên một học sinh. Tính xác suất chọn được một học sinh nữ.

A. 1/38        B. 10/19        C. 9/19        D. 19/9

Lời giải:

Đáp án: C

Chọn đáp án: C.

Gọi A là biến cố: "chọn được một học sinh nữ."

Bài 13: Một tổ học sinh có 7 nam và 3 nữ. Chọn ngẫu nhiên 2 người. Tính xác suất sao cho 2 người được chọn có đúng một người nữ.

A. 1/15        B. 7/15        C. 8/15        D. 1/5

Lời giải:

Đáp án: B

Chọn đáp án: B.

Gọi A là biến cố: "2 người được chọn có đúng một người nữ."

Bài 14: Chọn ngẫu nhiên một số có 2 chữ số từ các số 00 đến 99. Xác suất để có một con số tận cùng là 0 là:

A.0.1.        B. 0.2.        C. 0.3.        D. 0.4.

Lời giải:

Đáp án: A

Chọn A.

Phép thử : Chọn một số có hai chữ số bất kì

Ta có n(Ω)=100

Biến cố A : Chọn số lẻ và chia hết cho 9 là các số 09, 81, 27, 63, 45, 99

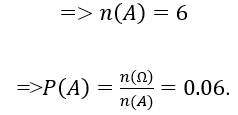
Bài 15: Chọn ngẫu nhiên một số có hai chữ số từ các số 00 đến 99. Xác suất để có một con số lẻ và chia hết cho 9 :

A. 0.12        B. 0.6.        C.0.06.        D. 0.01.

Lời giải:

Đáp án: C

Chọn C.

Phép thử : Chọn một số có hai chữ số bất kì

Ta có n(Ω)=100

Biến cố A : Chọn số lẻ và chia hết cho 9 là các số 09, 81, 27, 63, 45, 99

⇒ n(A)=6

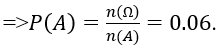
Bài 16: Từ ác chữ số 1,2,3,4 nhười ta lập các số tự nhiên có 3 chữ số khác nhau. Tính số phần tử không gian mẫu

A. 16        B. 24        C. 6        D. 4

Lời giải:

Đáp án: B

Ta lập được 4! =24 số

Bài 17: Từ các chữ số 1,2,3,4 người ta lập các số tự nhiên có 3 chữ số khác nhau.

Phát biểu biến cố A={123,234,124,134} dưới dạng mệnh đề

A. Số tự nhiên có ba chữ số được thành lập từ các chữ số 1,2,3,4

B. Số tự nhiên có ba chữ số được thành lập có chữ số đứng sau lớn hơn chữ số đứng trước

C. Số tự nhiên có ba chữ số được thành lập chia hết cho 2 hoặc 3

D. Số tự nhiên có ba chữ số được thành lập có chữ số tận cùng là 3 hoặc 4

Lời giải:

Đáp án: B

Ta thấy chữ số hàng chục lớn hơn chữ số hàng trăm, chữ số hàng đơn vị lớn hơn chữ số hàng chục chọn B

Bài 18: Một cái túi chứa 3 viên bi đỏ và 5 bi xanh, 6 viên bi vàng. Chọn ngẫu nhiên 3 viên bi. Xác suất để 3 viên bi có cả ba màu đỏ, xanh, vàng là:

A. 1/14        B. 45/182        C. 1/90        D. 1/364

Lời giải:

Đáp án: B

Xem việc tung con súc sắc là một phép thử ngẫu nhiên

Số lần thực hiện phép thử: N=100

Số lần xuất hiện của biến cố A: 12

Suy ra P(A)=12/ 100= 3/25

Số lần xuất hiện của biến cố B: 18

Suy ra P(B)= 18/ 100= 9/ 50

Số lần xuất hiện của biến cố C: 14+30+14=58

Suy ra P(B)= 58/ 100)= 29/ 50.

Bài 19: Gieo 3 con súc sắc cân đối, đồng chất và quan sát số chấm xuất hiện. Khi đó Xác suất để tổng số chấm xuất hiện trên mặt ba con súc sắc bằng 12 là

A. 25/216        B. 1/8        C. 1/6        D. 1/3

Lời giải:

Đáp án: A

1. Ta có:

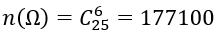
2. Ta có:

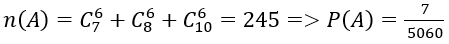
Ta có:

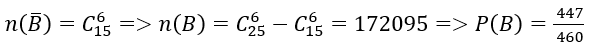
Ta có: Số cách lấy 6 viên bi cùng một màu: 245 cách

Số cách lấy 6 viên bi gồm hai màu:

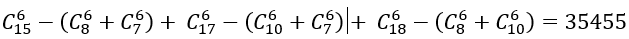
Suy ra n(C)=177100-35455-245=141400. Vậy P(C)=202/253.

Bài 20: Hai xạ thủ cùng bắn mỗi nhười một viên đạn vào bia một cách độc lập với nhau. Xác suất bắn trúng bia của hai xạ thủ lần lượt là 1/2 và 1/3

Tính xác suất của biến cố X:"cả hai xạ thủ đều bắn trúng bia"

A. 5/6        B. 1/6        C. 2/3        D. 1/3

Lời giải:

Đáp án: B

Gọi A là biến cố "Xạ thủ thứ i bắn trúng bia" i = 1,2.

Khi đó, P(A₁) =1/2; P(A₂) = 1/3; A₁ và A₂ độc lập với nhau

X =A₁∩ A₂ nên P(X) = P(A₁∩ A₂) = P(A₁.A₂) = P(A₁).P(A₂) = 1/6

Chọn đáp án là B

Bài 21: Lớp 11B có 25 đoàn viên trong đó có 10 nam và 15 nữ. Cho ngẫu nhiên 3 đoàn viên trong lớp để tham dự hội trại ngày 26 tháng 3. Tính xác suất để 3 đoàn viên được chọn có 2 nam và 1 nữ.

A. 3/115        B. 27/92        C. 9/92        D. 7/920

Lời giải:

Đáp án: D

Chọn 3 đoàn viên trong 25 đoàn viên thì có 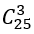cách chọn,

do đó ta có: n(Ω) = 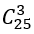= 2300 phần tử

Có 10 đoàn viên nam chọn 2 đoàn viên thì có 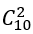cách chọn;

có 15 đoàn viên nữ chọn 1 nữ thì có 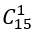cách chọn.

Gọi A là biến cố:"3 đoàn viên được chọn có 2 nam và 1 nữ" thì số phần tử của tập A là n(A)

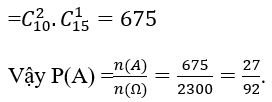
Bài 22: Một túi chứa 2 bi trắng và 3 bi đen. Rút ra 3 bi. Xác suất để được ít nhất 1 bi trắng là:

A. 1/5.        B. 1/10.        C. 9/10.        D. 4/5.

Lời giải:

Đáp án: C

Bài 23: Một hộp đựng 4 bi xanh và 6 bi đỏ lần lượt rút 2 viên bi. Xác suất để rút được một bi xanh và 1 bi đỏ là:

A. 2/15.        B. 6/25.        C. 8/25.        D. 4/15.

Lời giải:

Đáp án: D

Phép thử : Rút lần lượt hai viên bi

Ta có n(Ω)=9.10=90

Biến cố A : Rút được một bi xanh, một bi đỏ n(Ω)=4.6=24

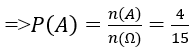
Bài 24: Một bình đựng 5 quả cầu xanh và 4 quả cầu đỏ và 3 quả cầu vàng. Chọn ngẫu nhiên 3 quả cầu. Xác suất để được 3 quả cầu khác màu là:

A. 3/5.        B. 3/7.        C. 3/11.        D. 3/14.

Lời giải:

Đáp án: C

Phép thử : Rút ngẫu nhiên ba quả cầu

Ta có n(Ω)=220

Biến cố A : Rút được ba qua cầu khác màu n(A)=5.4.3=60

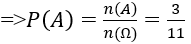
Bài 25: Một bình đựng 5 viên bi xanh và 3 viên bi đỏ (các viên bi chỉ khác nhau về màu sắc). Lấy ngẫu nhiên một viên bi, rồi lấy ngẫu nhiên một viên bi nữa. Khi tính xác suất của biến cố "Lấy lần thứ hai được một viên bi xanh", ta được kết quả

A. 5/8        B. 5/9        C. 5/7        D. 4/7

Lời giải:

Đáp án: A

Chọn A.

Gọi A là biến cố "Lấy lần thứ hai được một viên bi xanh". Có hai trường hợp xảy ra

Trường hợp 1. Lấy lần thứ nhất được bi xanh, lấy lần thứ hai cũng được một bi xanh. Xác suất trong trường hợp này là

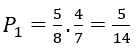
Trường hợp 2. Lấy lần thứ nhất được bi đỏ, lấy lần thứ hai được bi xanh. Xác suất trong trường hợp này là

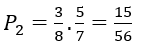
Vậy P(A)= P₁+ P₂=5/8

Bài 26: Một hộp có hai bi trắng được đánh số từ 1 đến 2, 3 viên bi xanh được đánh số từ 3 đến 5 và 2 viên bi đỏ được đánh số từ 6 đến 7. Lấy ngẫu nhiên hai viên bi:

Mô tả không gian mẫu

A. Ω={(m,n)|1 ≤ m ≤ 7,1 ≤ n ≤ 7}

B. Ω={(m,n)|1 ≤ m ≤ 7,1 ≤ n ≤ 7,m ≠ n}

C. Ω={(m,n)|1 ≤ m ≤ 5,6 ≤ n ≤ 7}

D. Ω={(m,n)|1 ≤ m ≤ 3,4 ≤ n ≤ 7}

Lời giải:

Đáp án: B

Mỗi viên bi đánh một số, nên 2 viên bi lấy ra mang số khác nhau. Vậy

Ω={(m,n)|1 ≤ n ≤ 7 và m ≠ n}

Bài 27: Một hộp có hai bi trắng được đánh số từ 1 đến 2, 3 viên bi xanh được đánh số từ 3 đến 5 và 2 viên bi đỏ được đánh số từ 6 đến 7. Lấy ngẫu nhiên hai viên bi:

Số phần tử của không gian mẫu là:

A. 49        B. 42        C. 10        D. 12

Lời giải:

Đáp án: B

Mỗi phần tử của không gian mẫu là một chỉnh hợp chập 2 của 7

vì vậy số phần tử của không gian mẫu là

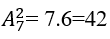
Bài 28: Một hộp có hai bi trắng được đánh số từ 1 đến 2, 3 viên bi xanh được đánh số từ 3 đến 5 và 2 viên bi đỏ được đánh số từ 6 đến 7. Lấy ngẫu nhiên hai viên bi:

Phát biểu biến cố M={(1,2),(3,4),(3,5),(4,5),(6,7)} dưới dạng mệnh đề

A. Hai bi lấy ra cùng màu trắng

B. Hai bi lấy ra cùng màu xanh

C. Hiệu hai số của hai bi không lớn hơn hai

D. Hai bi lấy ra cùng màu

Lời giải:

Đáp án: D

Bài 29: Chọn ngẫu nhiên 5 sản phẩm trong 10 sản phẩm. Biết rằng trong 10 sản phẩm đó có 2 phế phẩm. Tính xác suất để trong 5 sản phẩm được chọn có đúng 1 phế phẩm

A. 2/5        B. 5/.9        C. 2/9        D. 7/9

Lời giải:

Đáp án: B

Gọi C là biến cố:" trong 5 sản phẩm được chọn có đúng một phế phẩm"

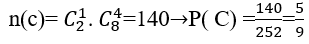
Bài 30: Trong một buổi liên hoan có 6 cặp nam nữ, trong đó có 3 cặp là vợ chồng. Chọn ngẫu nhiên 3 người trong số đó tham gia trò chơi

Tính xác suất để trong 3 người được chọn có đúng 1 người là nam

A. 1/4        B. 9/22        C. 1/11        D. 19/22

Lời giải:

Đáp án: B

Số khả năng chọn ngẫu nhiên 3 người từ 6*2= 12 người là

a. Gọi A là biến cố:" trong 3 người được chọn có đúng 1 nam"

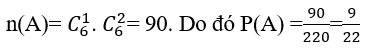
Bài 31: Trong một bài thi trắc nghiệm khách quan có 20 câu, mỗi câu có 4 phương án trả lời trong đó chỉ có 1 phương án đúng. Một học sinh không học bài nên làm bài bài bằng cách chọn ngẫu nhiên mỗi câu một phương án. Tính xác suất để học sinh đó trả lời đúng 10 câu?

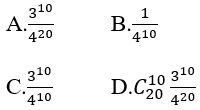
Lời giải:

Đáp án: D

Gọi A_i là biến cố:" học sinh chọn đúng ở câu i" i= 1,2,..,20

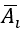
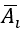
Ta có P(A_i) =1/4, thì là biến cố:" học sinh chọn sai ở câu i" i= 1,2,..,20 và P() = 1- P(A_i)= 3/4

Gọi X là biến cố:" Học sinh trả lời đúng 10 câu trong 20 câu"

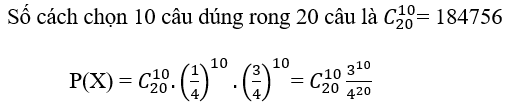
Bài 32: Có hai hộp bút chì. Hộp 1 có 3 bút đỏ và 4 bút xanh. Hộp II có 8 bút đỏ và 4 bút xanh. Chọn ngẫu nhiên từ mỗi hộp ra 1 bút. Tính xác suất để có 1 bút đỏ và 1 bút xanh.

A.1/12        B.1/6        C.7/12        D.11/24

Lời giải:

Đáp án: C

Gọi A là biến cố:" chọn bút đỏ ở hộ thứ i" i=1,2

B là biến cố:" chọn bút xanh ở hộp thứ i " i= 1,2

Ta có P(A₁)=3/12; P(A₂)=8/12 ; P(B₁) =9/12; P(B₂) =4/12

Gọi X là biến cố: " chọn được 1 bút đỏ và 1 bút xanh" thì X= A₁B₂∪ A₂ B₁

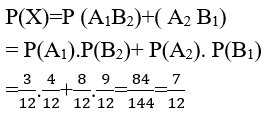
Bài 33: Một nhóm bạn có 4 bạn gồm 2 bạn Mạnh, Dũng và hai nữ là Hoa, Lan được xếp ngẫu nhiên trên một ghế dài. Kí hiệu (MDHL) là cách sắp xếp theo thứ tự: Mạnh, Dũng, Hoa, Lan

Tính số phần tử của không gian mẫu

A. 6        B. 24        C. 1        D. 4

Lời giải:

Đáp án: B

Mỗi cách xắp sêp 4 bạn vào 4 chỗ ngồi là một hoán vị của 4 phần tử. Vì vậy số phần tử của không gian mẫu là 4! =24

Bài 34: Một nhóm bạn có 4 bạn gồm 2 bạn Mạnh, Dũng và hai nữ là Hoa, Lan được xếp ngẫu nhiên trên một ghế dài. Kí hiệu (MDHL) là cách sắp xếp theo thứ tự: Mạnh, Dũng, Hoa, Lan

Xác định biến cố M:"xếp hai nam ngồi cạnh nhau"

A. M={(MDHL),(HMDL),(HLMD)}

B. M={(MDHL),(LMDH),(LHMD)}

C. M={(MDHL),(MDLH),(HMDL),(LMDH),(HLMD),(LHMD)}

D. M={(MDHL),(DMHL),(MDLH),(DMLH),(HMDL),(HDML),(LMDH),(LDMH),(HLMD),(HLDM),(LHMD),(LHDM)}

Lời giải:

Đáp án: D

Đánh số ghế theo thứ tự 1,2,3,4. Hai bạn nam ngồi cạnh nhau ở vị trí ( 1 và 2) hoặc (2 và 3) hoặc (3 và 4). Nếu hai bạn nam đổi chỗ cho nhau( giữ nguyên chỗ hai bạn nữ) thì ta có một cách xếp mới . Vì vậy cần chọn phương án D

Bài 35: Một nhóm bạn có 4 bạn gồm 2 bạn Mạnh, Dũng và hai nữ là Hoa, Lan được xếp ngẫu nhiên trên một ghế dài. Kí hiệu (MDHL) là cách sắp xếp theo thứ tự: Mạnh, Dũng, Hoa, Lan

Tìm số phần tử của biến cố N:"xếp nam và nữ ngồi xen kẽ nhau"

A.24        B.4        C.8        D.6

Lời giải:

Đáp án: C

Trường hợp 1: bạn nam ngồi đầu. khi dó 2 bạn nam xếp vào 2 chỗ ( số ghế 1 và 3), nữ xếp nốt vào hai chỗ còn lại ( ghế số 2 và 4), số cách xếp là 2!.2!=4

Trường hợp 2: bnạ nữ ngồi đầu. Tương tự có 4 cách xếp . Vậy theo quy tắc cộng số phần tử của biến cố N là 4+4=8

Bài 36: Gieo ngẫu nhiên ba đồng xu phân biệt một lần. Kí hiệu S, N lần lượt chỉ đồng xu lật sấp, lật ngửa

Hãy mô tả không gian mẫu

A.Ω={S,N,S}

B.Ω={SSS,SSN,SNS,NSS}

C.Ω={SSS,SSN,SNS,NSS,NNS,NSN,SNN,NNN}

D.Ω={NNN,NSN,SNS}

Lời giải:

Đáp án: C

Mỗi phần tử của không gian mẫu chỉ rõ ba đồng tiền xuất hiện ngẫu nhiên mặt sấp hay mặt ngửa. Vì vậy cần chọn phương án C

Bài 37: Chọn ngẫu nhiên 5 sản phẩm trong 10 sản phẩm. Biết rằng trong 10 sản phẩm đó có 2 phế phẩm.

Tính xác suất để trong 5 sản phẩm được chọn đó không có phế phẩm nào:

A.1/2        B.5/8        C.2/9        D.1/5

Lời giải:

Đáp án: C

Số khả năng chọn 5 sản phẩm trong 10 sản phẩm là

Gọi A là biến cố:" trong 5 sản phẩm được chọn không có phế phẩm nào"

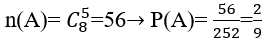
Bài 38: Chọn ngẫu nhiên 5 sản phẩm trong 10 sản phẩm. Biết rằng trong 10 sản phẩm đó có 2 phế phẩm. Tính xác suất để trong 5 sản phẩm được chọn có ít nhất 1 phế phẩm

A.1/2        B.3/8        C.7/9        D.4/5

Lời giải:

Đáp án: D

Gọi B là biến cố:" trong 5 sản phẩm được chọn có ít nhất 1 phế phẩm" thì

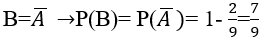
Bài 39: Một hộp có 5 viên bi đỏ và 9 viên bi xanh. Chọn ngẫu nhiên 2 viên bi. Xác suất để chọn được 2 viên bi khác màu là:

A. 14/35.        B. 45/91.        C. 46/91.        D. 15/22.

Lời giải:

Đáp án: B

Chọn B.

Gọi A là biến cố: "chọn được 2 viên bi khác màu."

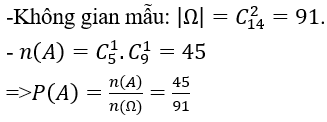
Bài 40: Một hộp chứa ba quả cầu trắng và hai quả cầu đen. Lấy ngẫu nhiên đồng thời hai quả. Xác suất để lấy được cả hai quả trắng là:

A. 2/10        B. 3/10        C. 4/10        D. 5/10

Lời giải:

Đáp án: B

Chọn B.

Gọi A là biến cố: "lấy được cả hai quả trắng."

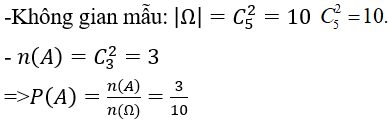
Bài 41: Có hai hộp thẻ. Hộp thứ nhất chứa các thẻ được đánh số từ 1 đến 5, hộp thứ hai chứa các thẻ được đánh số từ 6 đến 9. Lấy ngẫu nhiên ở mỗi hợp 1 thẻ

Hãy mô tả không gian mẫu, kí hiệu "ab" thể hiện hộp thứ nhất lấy thể đánh số a, hộp thứ hai lấy thẻ đánh số b.

A. Ω={16,27,38,49,56}

B. Ω={19,28,37,46,57}

C. Ω={16,17,18,19,26,27,28,29,36,37,38,39,46,47,48,49,56,57,58,59}

D. Ω={61,62,63,64,65,71,72,73,74,75,81,82,83,84,85,91,92,92,94,95}

Lời giải:

Đáp án: C

Ω={16,17,18,19,26,27,28,29,36,37,38,39,46,47,48,49,56,57,58,59}

Vì hộp thứ nhất chứa các thẻ được đánh số từ 1 đến 5, hộp thứ hai chứa các thẻ được đánh số từ 6 đến 9

Bài 42: Có hai hộp thẻ. Hộp thứ nhất chứa các thẻ được đánh số từ 1 đến 5, hộp thứ hai chứa các thẻ được đánh số từ 6 đến 9. Lấy ngẫu nhiên ở mỗi hợp 1 thẻ

Xác định biến cố M:"tổng các số ở hai thẻ lấy ra là số nguyên tố"

A. M={16,38,49,56}

B. M={16,29,38,47,49,56,58}

C. M={61,74,92,94,65}

D. M={16,38,56}

Lời giải:

Đáp án: B

M={16,29,38,47,49,56,58} tổng các chữ số là số nguyên tố

Bài 43: Có ba xạ thủ đi săn đêm. Gọi A_k là biến cố:"xạ thủ thứ k bắn trúng đích" với k = 1,2,3. Hãy dùng các phép toán nêu các biến cố biểu thị qua A₁,A₂,A₃.

Biến cố M: "không có xạ thủ nào bắn trúng đích"

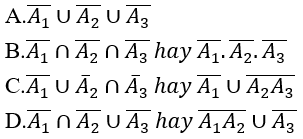
Lời giải:

Đáp án: B

Theo bài ra biến cố A_k: " xạ thủ thứ k bắn trúng đích ", với k=1,2,3 thì biến cố đối 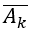" xạ thứ thứ k bắn trượt "

Biến cố M " không có xạ thủ nào bắn trúng đích" , tức là cả ba xạ thủ đều bắn trượt nên

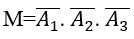
Bài 44: Có ba xạ thủ đi săn đêm. Gọi A_k là biến cố:"xạ thủ thứ k bắn trúng đích" với k = 1,2,3. Hãy dùng các phép toán nêu các biến cố biểu thị qua A₁,A₂,A₃.

Biến cố N:"có đúng hai xạ thủ trúng đích"

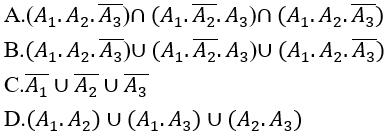
Lời giải:

Đáp án: B

Biến cố N: " có đúng hai xạ thủ bắn trúng đích" tức là trong ba xạ thủ có hai người bắn trúng và một người bắn trượt

Bài 45: Gieo hai con súc sắc. Xác suất để tổng số chấm trên hai mặt chia hết cho 3 là:

A. 13/36        B. 11/36.        C. 1/3.        D. 1/6.

Lời giải:

Đáp án: C

Chọn C.

Số phần tử không gian mẫu:n(Ω)=6.6=36

Biến cố tổng hai mặt chia hết cho là:

A={(1,2);(1,5);(2,1);(2,4);(3,3);(3,6);(4,2);(4,5);(5,1);(5,4);(6,3);(6,6)}

Nên n(A)=12

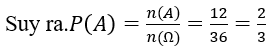
Bài 46: Gieo ba con súc sắc. Xác suất để nhiều nhất hai mặt 5 là:

A. 5/72.        B. 1/216        C. 1/72.        D.1

Lời giải:

Đáp án: D

Chọn D.

Số phần tử không gian mẫu: n(Ω)=6.6.6=216

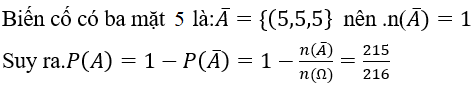
Bài 47: Rút ra một lá bài từ bộ bài 52 lá. Xác suất để được lá át (A) là:

A. 2/13.        B. 1/169.        C. 1/13.        D. 3/4 .

Lời giải:

Đáp án: C

Chọn C.

Số phần tử không gian mẫu: : n(Ω)=52

Số phần tử của biến cố xuất hiện lá ách: : n(A)=4

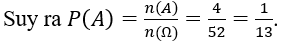
Bài 48: Rút ra một lá bài từ bộ bài 52 lá. Xác suất để được lá ách (A) hay lá rô là:

A. 1/52.        B. 2/13.        C. 4/13.        D. 17/52.

Lời giải:

Đáp án: C

Chọn C.

Số phần tử không gian mẫu: : n(Ω)=52

Số phần tử của biến cố xuất hiện lá ách: : n(A)=4

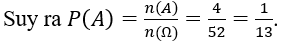
Bài 49: Gieo hai đồng tiền một lần. Kí hiệu S,N để chỉ đông tiền lật sấp, lật ngửa.

Mô tả không gian mẫu

A. Ω={SN,NS}

B. Ω={NN,SS}

C. Ω={S,N}

D. Ω={SN,NS,SS,NN}

Lời giải:

Đáp án: D

Ω={SN,NS,SS,NN}

Bài 50: Gieo hai đồng tiền một lần. Kí hiệu S,N để chỉ đông tiền lật sấp, lật ngửa.

Xác định biến cố M: "hai đông tiền xuất hiện hai mặt không giống nhau"

A. M={NN,SS}

B. M={NS,SN}

C. M={NS,NN}

D. M={SS,SN}

Lời giải:

Đáp án: B

M={NS,SN}

Bài 51: Một chiếc máy có ba động cơ I,II,III hoạt động độc lập với nhau. Xác xuất để động cơ I,II,III chạy tốt tương ứng là 0,7;0,8;0,9.

Xác suất để cả 3 động cơ chạy tốt

A.0.006

B.0.496

C.0.504

D.0.994

Lời giải:

Đáp án: D

Gọi A_i là biến cố:" động cơ i chạy tốt" i=1,2,3

P(A₁)= 0,7 ; P(A₂).= 0,8 ; P(A₃)=0,9 và A₁, A₂, A₃ độc lập với nhau

A₁, A₂, A₃ là biến cố:" cả 3 biến cố đều chạy tốt "

P(A₁. A₂. A₃)= P(A₁). P(A₂). P(A₃)= 0,504

Bài 52: Một bộ bài tú lơ khơ gồm 53 con, lấy ngẫu nhiên lần lượt có hoàn lại từng con cho đến khi lần đầu tiên lấy được con át thì dừng

Tính xác suất sao cho quá trình dừng lại ở ngay lần thứ nhất

A.12/13        B.1/13        C.1/4        D.0

Lời giải:

Đáp án: B

Kí hiệu A_k: " lần thứ k lấy được con át" k ≥ 1

Bài 53: Trong một buổi liên hoan có 6 cặp nam nữ, trong đó có 3 cặp là vợ chồng. Chọn ngẫu nhiên 3 người trong số đó tham gia trò chơi

Tính xác suất để trong 3 người dược chọn không có cặp vợ chồng nào

A.1/4        B.9/22        C.1/11        D.19/22

Lời giải:

Đáp án: D

Gọi B là biến cố :" trong 3 người được chọn không có cặp vợ chồng nào" thì 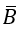là biến cố :" có đúng một cặp vợ chồng trong ba người được chọn"

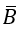
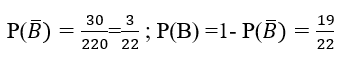
Ta có n() = 3.10=30( vì có 3 cách chọn cặp vợ chồng, và 10 cách chọn người thứ 3 trong số 10 người còn lại) nên

Bài 54: Một lớp học có 40 học sinh trong đó coa 15 học sinh giỏi Toán, 10 học sinh giỏi Văn và 5 học sinh giỏi cả Văn và Toán. Chọn ngẫu nhiên một học sinh.

Xác suất của biến cố A:"học sinh được chọn giỏi Toán" là:

A.1/40        B.8/3        C.3/8        D.1/8

Lời giải:

Đáp án: C

Ta có n(Ω) = 40

Rõ ràng n(A) = 15 nên P(A) = 15/40 = 3/8

Chọn đáp án là C

Bài 55: Lấy ngẫu nhiên 1 thẻ từ 1 hộp 30 thẻ được đánh số từ 1 đến 30.

Tính xác suất để thẻ được lấy ghi số 6

A.1/30        B.1/5        C.6        D.1/6

Lời giải:

Đáp án: A

không gian mẫu Ω={1,2,..30}. kí hiệu A là biến cố " thẻ lấy ra ghi số 6", B là biến cố "thẻ lấy ra ghi số chia hết cho 5"

A={6}, n(A) =1,n(Ω) = 30

⇒ P(A) =1/30

Chọn đáp án A

Bài 56: Trong một buổi liên hoan có 6 cặp nam nữ, trong đó có 3 cặp là vợ chồng. Chọn ngẫu nhiên 3 người trong số đó tham gia trò chơi

Tính xác suất để trong 3 người được chọn có đúng 1 người là nam

A. 1/4        B. 9/22        C. 1/11        D. 19/22

Lời giải:

Đáp án: B

Số khả năng chọn ngẫu nhiên 3 người từ 6*2= 12 người là

a. Gọi A là biến cố:" trong 3 người được chọn có đúng 1 nam"

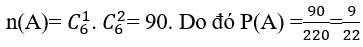
Bài 57: Một hộp chứa ba quả cầu trắng và hai quả cầu đen. Lấy ngẫu nhiên đồng thời hai quả. Xác suất để lấy được cả hai quả trắng là:

A. 2/10        B. 3/10        C. 4/10        D. 5/10

Lời giải:

Đáp án: B

Chọn B.

Gọi A là biến cố: "lấy được cả hai quả trắng."

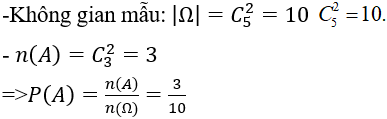
Bài 58: Một túi chứa 2 bi trắng và 3 bi đen. Rút ra 3 bi. Xác suất để được ít nhất 1 bi trắng là:

A. 1/5.        B. 1/10.        C. 9/10.        D. 4/5.

Lời giải:

Đáp án: C

Số phần tử của không gian mẫu: n(Ω)=10

Bài 59: Từ ác chữ số 1,2,3,4 nhười ta lập các số tự nhiên có 3 chữ số khác nhau. Tính số phần tử không gian mẫu

A. 16        B. 24        C. 6        D. 4

Lời giải:

Đáp án: B

Ta lập được 4!=24 số

Bài 60: Trong một buổi liên hoan có 6 cặp nam nữ, trong đó có 3 cặp là vợ chồng. Chọn ngẫu nhiên 3 người trong số đó tham gia trò chơi

Tính xác suất để trong 3 người dược chọn không có cặp vợ chồng nào

A. 1/4        B. 9/22        C. 1/11        D. 19/22

Lời giải:

Đáp án: D

Gọi B là biến cố :" trong 3 người được chọn không có cặp vợ chồng nào" thì 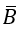là biến cố :" có đúng một cặp vợ chồng trong ba người được chọn"

Ta có n() = 3.10=30( vì có 3 cách chọn cặp vợ chồng, và 10 cách chọn người thứ 3 trong số 10 người còn lại) nên