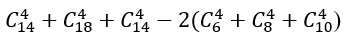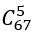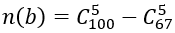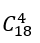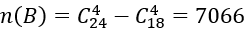Cách xác định phép thử, không gian mẫu và biến cố cực hay - Toán lớp 11
Cách xác định phép thử, không gian mẫu và biến cố cực hay
Với Cách xác định phép thử, không gian mẫu và biến cố cực hay Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập xác định phép thử, không gian mẫu và biến cố từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải & Ví dụ
Để xác định không gian mẫu và biến cố ta thường sử dụng các cách sau
Cách 1: Liệt kê các phần tử của không gian mẫu và biến cố rồi chúng ta đếm.
Cách 2: Sử dụng các quy tắc đếm để xác định số phần tử của không gian mẫu và biến cố.
Ví dụ minh họa
Bài 1: Trong một chiếc hộp đựng 6 viên bi đỏ, 8 viên bi xanh, 10 viên bi trắng. Lấy ngẫu nhiên 4 viên bi. Tính số phần tử của:
1. Không gian mẫu
2. Các biến cố:
A: " 4 viên bi lấy ra có đúng hai viên bi màu trắng"
B: " 4 viên bi lấy ra có ít nhất một viên bi màu đỏ"
C: " 4 viên bi lấy ra có đủ 3 màu"
Đáp án và hướng dẫn giải
1.
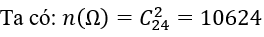
2. Số cách chọn 4 viên bi có đúng hai viên bị màu trắng là:
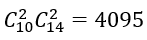
Suy ra: n(Ω)=4095
Số cách lấy 4 viên bi mà không có viên bi màu đỏ được chọn là:
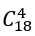
Suy ra :
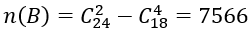
Số cách lấy 4 viên bi chỉ có một màu là:
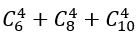
Số cách lấy 4 viên bi có đúng hai màu là:
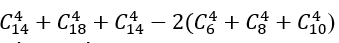
Số cách lấy 4 viên bị có đủ ba màu là:
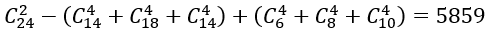
Suy ra n(C)=5859
Bài 2: Một xạ thủ bắn liên tục 4 phát đạn vào bia. Gọi Ak là các biến cố " xạ thủ bắn trúng lần thứ k" với k = 1,2,3,4. Hãy biểu diễn các biến cố sau qua các biến cố A1, A2, A3, A4
A: "Lần thứ tư mới bắn trúng bia’’
B: "Bắn trúng bia ít nhất một lần’’
C: " Chỉ bắn trúng bia hai lần’’
Đáp án và hướng dẫn giải
Ta có: Giả sử 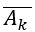
Do đó:
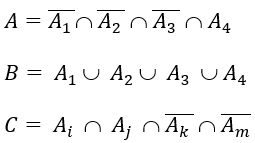
với i,k,k,m ∈ {1,2,3,4} và đôi một khác nhau.

B. Bài tập vận dụng
Bài 1: Xét phép thử tung con súc sắc 6 mặt hai lần. Tính số phần tử của:
1. Xác định không gian mẫu
2. Các biến cố:
A:" số chấm xuất hiện ở cả hai lần tung giống nhau"
B:" Tổng số chấm xuất hiện ở hai lần tung chia hết cho 3"
C: " Số chấm xuất hiện ở lần một lớn hơn số chấm xuất hiện ở lần hai".
Lời giải:
1. Không gian mẫu gồm các bộ (i,j) trong đó i,j ∈ {1,2,3,4,5,6}
i nhận 6 giá trị, j cũng nhận 6 giá trị nên có 6.6=36 bộ (i,j)
Vậy Ω={(i,j)│i,j=1,2,3,4,5,6} và n(Ω)=36 .
2. Ta có: A={(1,1);(2,2);(3,3);(4,4);(5,5);(6,6)}, n(A)=6
Xét các cặp (i,j) với i,j ∈ {1,2,3,4,5,6} mà i+j chia hết cho 3
Ta có các cặp có tổng chia hết cho 3 là (1,2);(1,5);(2,4);(3,3);(3,6);(4,5)
Hơn nữa mỗi cặp (trừ cặp (3,3)) khi hoán vị ta được một cặp thỏa yêu cầu bài toán.
Vậy n(B) = 11.
Số các cặp i,j (i > j) là (2,1);(3,1);(3,2);(4,1);(4,2);(4,3);(5,1);(5,2);(5,3);(5,4);(6,1);(6,2);(6,3);(6,4),(6,5).
Vậy n(C) = 15.
Bài 2: Gieo một đồng tiền 5 lần. Xác định và tính số phần tử của
1. Không gian mẫu
2. Các biến cố:
A: " Lần đầu tiên xuất hiện mặt ngửa"
B: " Mặt sấp xuất hiện ít nhất một lần"
C: " Số lần mặt sấp xuất hiện nhiều hơn mặt ngửa"
Lời giải:
1. Không gian mẫu
2. Các biến cố:
A: " 4 viên bi lấy ra có đúng hai viên bi màu trắng"
B: " 4 viên bi lấy ra có ít nhất một viên bi màu đỏ"
Lời giải:
Bài 3: Có 100 tấm thẻ được đánh số từ 1 đến 100. Lấy ngẫu nhiên 5 thẻ. Tính số phần tử của:
1. Không gian mẫu
2. Các biến cố:
A: " Số ghi trên các tấm thẻ được chọn là số chẵn"
B: " Có ít nhất một số ghi trên thẻ được chọn chia hết cho 3".
Lời giải:
1.
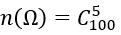
2. Trong 100 tấm thẻ có 50 tấm được ghi các số chẵn, do đó
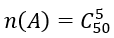
Từ 1 đến 100 có 33 số chia hết cho 3. Do đó, số cách chọn 5 tấm thẻ mà không có tấm thẻ nào ghi số chia hết cho 3 là:
Vậy
Bài 4: Trong một chiếc hộp đựng 6 viên bi đỏ, 8 viên bi xanh, 10 viên bi trắng. Lấy ngẫu nhiên 4 viên bi. Tính số phần tử của:
1. Không gian mẫu
2. Các biến cố:
A: " 4 viên bi lấy ra có đúng hai viên bi màu trắng"
B: " 4 viên bi lấy ra có ít nhất một viên bi màu đỏ"
Lời giải:
1.
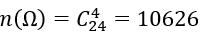
2. Số cách chọn 4 viên bi có đúng hai viên bị màu trắng là:
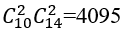
Suy ra: n(A)=4095.
Số cách lấy 4 viên bi mà không có viên bi màu đỏ được chọn là:
Suy ra :
Số cách lấy 4 viên bi chỉ có một màu là:
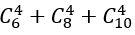
Số cách lấy 4 viên bi có đúng hai màu là: