Cách chứng minh hai mặt phẳng song song cực hay - Toán lớp 11

---

Cách chứng minh hai mặt phẳng song song cực hay

Với Cách chứng minh hai mặt phẳng song song cực hay Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập hai mặt phẳng song song từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải

Để chứng minh hai mặt phẳng song song ta có thể thực hiện theo một trong hai hướng sau:

- Chứng minh trong mặt phẳng này có hai đường thẳng cắt nhau cùng song song với mặt phẳng kia.

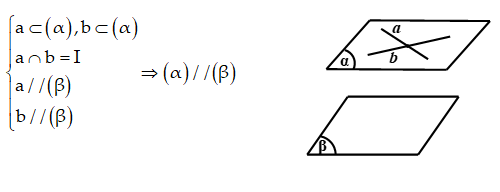
- Chứng minh hai mặt phẳng đó cùng song song với măt mặt phẳng thứ ba

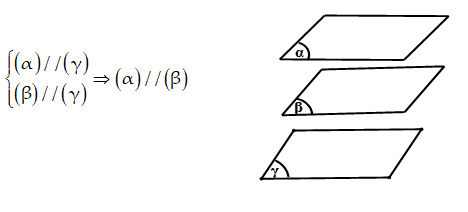
B. Ví dụ minh họa

Ví dụ 1: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O. Gọi M; N: I theo thứ tự là trung điểm của SA; SD và AB. Khẳng định nào sau đây đúng?

A. (NOM) cắt (OPM)

B. (MON) // (SBC)

C. (PON) ∩ (MNP) = NP

D. (NMP) // (SBD)

Lời giải

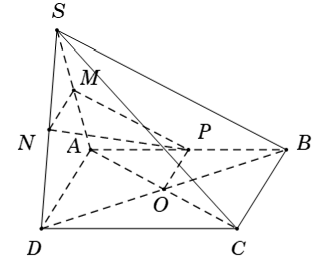
   + Ta có MN là đường trung bình của tam giác SAD suy ra: MN // AD  (1). Và OP là đường trung bình của tam giác ABC suy ra: OP // BC // AD   (2)

Từ (1)và (2) suy ra : MN // OP // AD nên 4 điểm M; N; O; P đồng phẳng

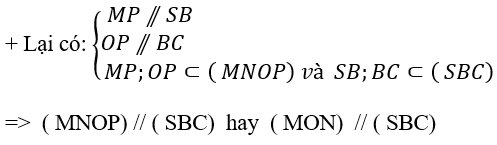
Chọn B

Ví dụ 2: Cho hình lăng trụ ABC. A’B’C’. Gọi H là trung điểm của A’B’. Đường thẳng B’C song song với mặt phẳng nào sau đây?

A. (AHC’)        B. (AA’H)        C. (HAB)        D. (HA’C)

Lời giải

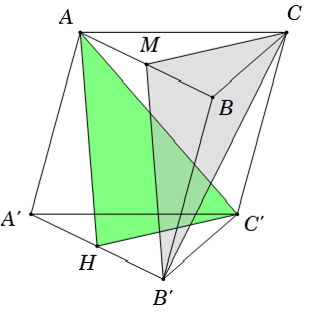
   + Gọi M là trung điểm của AB suy ra: AM B’H là hình bình hành

⇒ MB’ // AH nên MB’ // mp(AHC’)   (1)

   + Vì MH là đường trung bình của hình bình hành ABB’A’ suy ra MH song song và bằng BB’ nên MH song song và bằng CC’

⇒ MHC’C là hình hình hành

⇒ MC // HC’ nên MC // (AHC’)   (2)

Từ (1) và (2) , suy ra (B’MC) // (AHC’)

⇒ B’C // (AHC’)

Chọn A

Ví dụ 3: Cho hình lăng trụ ABC. A’B’C’. Gọi H là trung điểm của A’B’. Mặt phẳng (AHC’) song song với đường thẳng nào sau đây?

A. CB’        B. BB’        C. BC         D. BA’

Lời giải

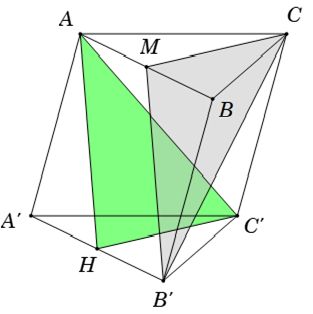
   + Gọi M là trung điểm của AB suy ra tứ giác AMB’H là hình bình hành

⇒ MB’ // AH nên MB’ // (AHC’)   (1)

   + Vì MH là đường trung bình của hình bình hành ABB’A’ suy ra MH song song và bằng BB’ nên MH song song và bằng CC’

⇒ MHC’C là hình hình hành

⇒ MC // HC’ và MC // (AHC’)   (2)

Từ (1) và (2) , suy ra (B’MC) // (AHC’)

⇒ B’C // (AHC’)

Chọn A

Ví dụ 4: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O , gọi M và N lần lượt là trung điểm của SA; SD. Chọn mệnh đề sai?

A. OM // mp(SBC)

B. ON // mp(SAB)

C. (OMN) // (SBC)

D. (OMN) và (SBC) cắt nhau

Lời giải

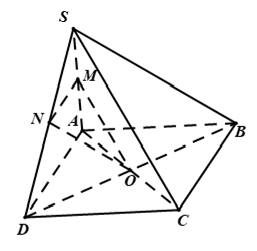
   + Ta có M và O lần lượt là trung điểm của SA và AC

⇒ OM là đường trung bình của tam giác SAC

⇒ OM // SC

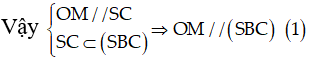
⇒ A đúng

   + Tương tự, N và O lần lượt là trung điểm của SD và BD

⇒ ON là đường trung bình của tam giác SBD

⇒ ON // SB

Chọn D

Ví dụ 5: Cho hình bình hành ABCD. Vẽ các tia Ax; By, Cz, Dt song song, cùng hướng nhau và không nằm trong mp (ABCD). Mp (α) cắt Ax;By, Cz, Dt lần lượt tại A’, B’,C’, D’. Khẳng định nào sau đây sai?

A. A’B’C’D’ là hình bình hành

B. mp(AA’B’B) // (DD’C’C)

C. AA’ = CC’ và BB’ = DD'

D. OO’ // AA’

Trong đó O là tâm hình bình hành ABCD , O’ là giao điểm của A’C’ và B’D’

Lời giải

Chọn C

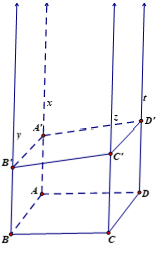
Ta xét các phương án:

   + Phương án B:

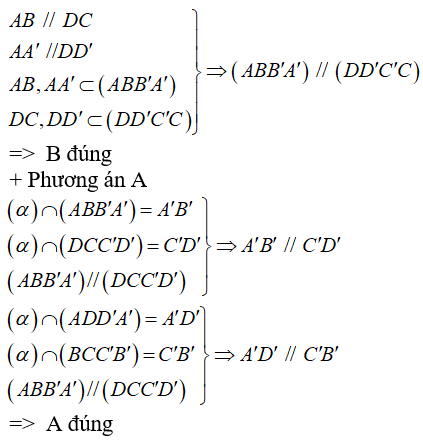
   + Phương án D:

Do O và O’ lần lượt là trung điểm của AC và A’C’ nên OO’ là đường trung bình trong hình thang AA’C’C. Do đó: OO’ // AA’

⇒ D đúng

Ví dụ 6: Cho hai hình vuông ABCD và ABEF ở trong hai mặt phẳng khác nhau. Tìm mệnh đề đúng ?

A. (CBE) // (ADF)

B. (ADB) // (CEF)

C. (CDF) // (ABE)

D. Không có hai mặt phẳng nào song song

Lời giải

   + Do ABCD là hình vuông nên: BC // AD

   + Do ABEF là hình vuông nên: BE // AF

   + Xét hai mp(CBE) và (ADF) có:

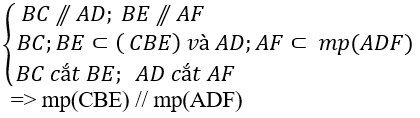
Chọn A

Ví dụ 7: Cho hình lăng trụ ABC.A1B1C1. Trong các khẳng định sau, khẳng định nào sai?

A. (ABC) // (A₁B₁C₁)

B. AA₁ // (BCC₁)

C. AB // (A₁B₁C₁)

D. AA₁BB₁ là hình chữ nhật

Lời giải

Chọn D

Vì theo tính chất của hình lăng trụ thì mặt bên AA₁B₁B là hình bình hành, còn nó là hình chữ nhật nếu ABC. A₁B₁C₁ là hình lăng trụ đứng.

Ví dụ 8: Cho hình hộp ABCD.A₁B₁C₁D₁. Khẳng định nào dưới đây là sai?

A. ABCD là hình bình hành

B. Các đường thẳng A₁C; AC₁; DB₁; D₁B đồng quy

C. (ADD₁A₁) // (BCC₁B₁)

D. AD₁CB là hình chữ nhật

Lời giải

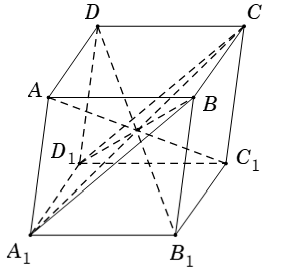
Dựa vào hình vẽ và tính chất của hình hộp chữ nhật, ta thấy rằng:

- Hình hộp có đáy ABCD là hình bình hành

- Các đường thẳng A₁C; AC₁; DB₁; D₁B cắt nhau tại tâm của hình hộp

- Hai mặt bên ( ADD₁A₁) và ( BCC₁B₁) đối diện và song song với nhau

- AD₁ và CB là hai đường thẳng chéo nhau suy ra AD1CB không phải là hình chữ nhật

Chọn D

Ví dụ 9: Cho hình hộp ABCD.A’B’C’D’. Gọi M ; P và Q lần lượt là trung điểm của AB ; CD và C’D’. Gọi N là trung điểm của AM. Tìm mệnh đề đúng ?

A. (NPC’) // (ADC)

B. (MCC’) // (NPQ)

C. (PMC’) // (DNB’)

D. (MCC’) // (APQ)

Lời giải

Chọn D

   + Xét tứ giác AMCP có:

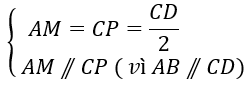
⇒ Tứ giác AMCP là hình bình hành

⇒ AP // MC

   + Xét hình bình hành CDD’C’ có P và Q lần lượt là trung điểm của CD và C’D’

⇒ PQ là đường trung bình của hình bình hành CDD’C’

⇒ PQ // CC’ // DD’

   + Xét mp (MCC’) và mp (APQ) có:

Ví dụ 10: Cho hình hộp ABCD.A’B’C’D’. Gọi O và O’ lần lượt là tâm của hình bình hành ABCD và A’B’C’D’. Gọi G là giao điểm của CD’và C’D. Tìm mệnh đề đúng ?

A. (OAG) // (O’CC’)

B. (OBG) // (PAO’)

C. (ODG) // (AO’D’)

D. Tất cả sai

Lời giải

Chọn C

   + Hình bình hành có hai đường chéo cắt nhau tại trung điểm mỗi đường

⇒ O là trung điểm AC và G là trung điểm CD’

Xét tam giác CAD’ có O và G lần lượt là trung điểm của AC và CD’

⇒ OG là đường trung bình của tam giác CAD’ nên OG // AD’

   + Do O và O’ là tâm của hình bình hành ABCD; A’B’C’D’ nên: OD // O’D’

   + Xét mp (ODG) và mp (AO’D’) có

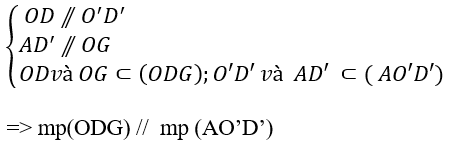
C. Bài tập trắc nghiệm

Câu 1: Cho hình lăng trụ ABC.A’B’C’. Gọi H là trung điểm của A’B’. Đường thẳng B’C song song với mặt phẳng nào sau đây ?

A. (AHC’)        B. (AA’H)        C. (HAB)        D.(HA’C’)

Lời giải:

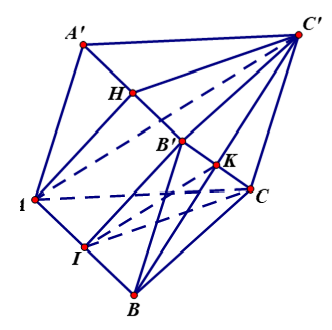
Chọn A

Gọi K là giao điểm của B’C và BC’, gọi I là trung điểm của BA

   + Do HB’ = AI = AB/2 và HB’ // AI

⇒ tứ giác AHB’I là hình bình hành.

⇒ AH // B’I  (1)

   + Xét tam giác ABC’ có I và K lần lượt là trung điểm của AB và BC’.

⇒ IK là đường trung bình của tam giác ABC’

Nên IK // AC’    (2)

   + Từ (1) và (2) suy ra: (AHC’) // (B’CI)

Mà B’C ⊂ (B’CI)

⇒ B’C // mp(AHC’)

Câu 2: Cho hình hộp ABCD.A’B’C’D’. Mặt phẳng (AB’D’)song song với mặt phẳng nào trong các mặt phẳng sau đây?

A. (BCA’)       B. (BC’D)       C. (A’C’C)       D. (BDA’)

Lời giải:

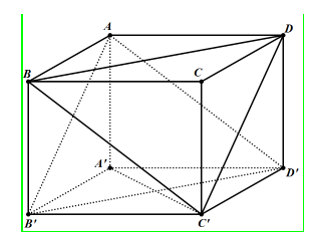
Chọn B

   + Do BDD’B’ là hình bình hành nên BD // B’D’   (1)

   + Do ADC’B’ là hình bình hành nên AB’ // DC’   (2)

Từ (1) và (2) suy ra: mp(AB’D’) // mp(BC’D)

Câu 3: Cho hình chóp S.ABCD. Gọi A’,B’,C’,D’ lần lượt là trung điểm của các cạnh SA, SB, SC và SD. Chọn mệnh đề sai ?

A. A’B’ // (ABCD)

B. A’C’ // (ABCD)

C. A’C’ // BD

D. (ACD) // (A’B’C’)

Lời giải:

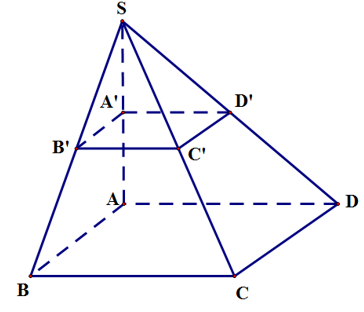
Chọn C

   + Do A’ và B’ lần lượt là trung điểm của SA và SB

⇒ A’B’ là đường trung bình của tam giác SAB và A’B’ // AB

Mà AB ⊂ (ABCD) nên A’B’ // (ABCD)   (1)

⇒ A đúng

   + Do A’ và C’ lần lượt là trung điểm của SA và SC

⇒ A’C’ là đường trung bình của tam giác SAC và A’C’ // AC

Mà AC ⊂ (ABCD) nên A’C’ // (ABCD)  (2)

⇒ B đúng

   + Từ (1) và (2) và kết hợp với A’B’ và A’C’ là hai đường thẳng cắt nhau tại A’ và cùng thuộc mp(A’B’C’D’) ta suy ra: mp(ABCD) // mp(A’B’C’D’)

⇒ D đúng

Câu 4: Cho lăng trụ ABC.A’B’C’. Gọi G và G’ lần lượt là trọng tâm tam giác ABC và A’B’C’. Gọi M và M’ lần lượt là trung điểm của BC và B’C’. Tìm mặt phẳng song song với mp(CA’M’).

A. mp(AMB’)

B. mp(GMC’)

C. mp(GBG’)

D. mp(AGA’)

Lời giải:

   + Xét tứ giác CMB’M’ có:

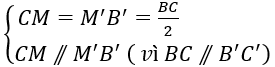
=> Tứ giác CMB’M’ là hình bình hành

=> CM’// MB’.

   + Xét tứ giác CBB’C’ có M và M’ lần lượt là trung điểm của BC; B’C’

=> MM’ là đường trung bình của CBB’C’ và MM’// BB’; MM’= BB’

⇒ AA’// MM’và AA’= MM’ ( chú ý tính chất hình lăng trụ)

⇒ Tứ giác AMM’A’ là hình bình hành.

⇒ AM // A’M’

   + xét hai mp(CA’M’) và mp(AMB’):

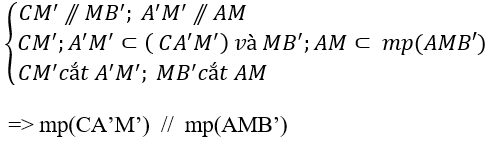
Chọn A

Câu 5: Cho hai hình vuông ABCD và ABEF ở trong 2 mặt phẳng khác nhau. Trên các đường chéo AC và BF lần lượt lấy các điểm M; N sao cho AM = BN. Các đường thẳng song song với AB vẽ từ M và N lần lượt cắt AD; AF tại M’; N’. Tìm mặt phẳng song song với (DEF)

A. (NN’C)        B. (AMM’)       C. (BMC)       D. (MNN’M’)

Lời giải:

   + Nhận xét: Hai hình vuông ABCD và ABEF có chung cạnh AB nên hai hình vuông này có độ dài các cạnh bằng nhau

⇒ Độ dài các đường chéo bằng nhau: AC = BF

   + Xét tam giác ACD có MM’ // CD // AB nên:

AM'/AD = AM/AC (định lí Ta-let)  (1)

   + Xét tam giác FAB có NN’ // AB nên:

BN/BF = AN'/AF (định lí Ta-let)  (2)

Mà BN = AM và AC = BF   (3)’

Từ (1); (2); (3) suy ra:

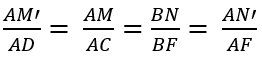
Câu 6: Cho hình hộp ABCD.A’B’C’D’ có các cạnh bên AA’; BB’; CC’ và DD’. Khẳng định nào dưới đây sai?

A. (AA’B’B) // (DD’C’C)

B. (BA’D’) // (ADC’)

C. A’B’CD là hình bình hành

D. BB’D’D là một tứ giác

Lời giải:

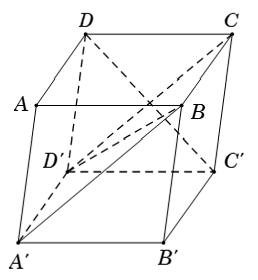
Dựa vào hình vẽ dưới và tính chất của hình hộp, ta thấy rằng:

- Hai mặt bên (AA’B’B) và (DD’C’C) đối diện, song song với nhau

- Hình hộp có hai đáy (ABCD) ; (A’B’C’D’) là hình bình hành

⇒ A’B’ = CD và A’B’ // CD

suy ra A’B’CD là hình hình hành.

- BD // B’D’ suy ra B; B’; D; D’ đồng phẳng nên BB’D’D là tứ giác

- Mặt phẳng (BA’D’) chứa đường thẳng CD’ mà CD’ cắt C’D suy ra (BA’D’) không song song với mặt phẳng (AD’C)

Chọn B

Câu 7: Cho lăng trụ ABC.A’B’C’. Gọi M; N và P lần lượt là trung điểm của AA’; BB’ và CC’. Tìm mệnh đề sai?

A. BP // mp (A’NC’)

B. mp(MPB) // mp(A’C’N)

C. mp(ABC) // mp(A’B’C’)

D. A’N // mp(ABC)

Lời giải:

   + Ta có ABC.A’B’C’ là hình lăng trụ nên mp(ABC) // mp(A’B’C’) (tính chất hình lăng trụ). Nên C đúng.

   + Xét tứ giác BNB’P có:

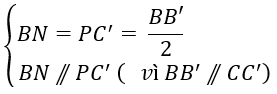
⇒ tứ giác BNC’P là hình bình hành

⇒ BP // NC’

Mà NC’ ⊂ mp(A’NC’) nên BP // mp(A’NC’)

⇒ A đúng.

   + Do M và P lần lượt là trung điểm của AA’ và CC’

⇒ MP // AC // A’C’

   + Xét mp(MPB) và mp(A’C’N) có:

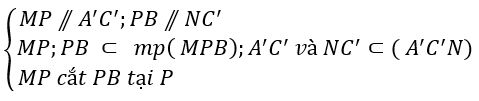
⇒ mp(MPB) // mp(A’C’N)

⇒ B đúng

⇒ D sai

Chọn D

Câu 8: Cho hình lăng trụ ABC.A’B’C’. Gọi M và N lần lượt là trung điểm của BB’ và CC’. Gọi Δ là giao tuyến của hai mặt phẳng (AMN) và (A’B’C’) Khẳng định nào sau đây đúng?

A. Δ // AB         B. Δ // AC         C. Δ // BC         D. Δ // AA'

Lời giải:

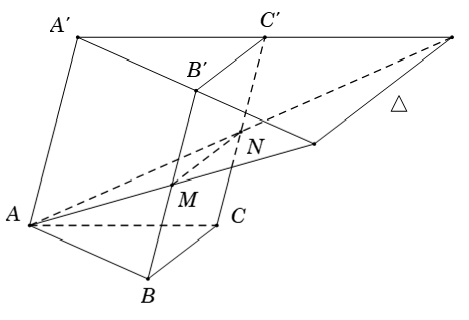
Ta có:

MN ⊂ (AMN)

B'C' ⊂ (A'B'C')

MN || B'C'

⇒ Δ là giao tuyến của hai mặt phẳng (AMN) và (A’B’C’) sẽ song song với MN và B’C’

Suy ra Δ // BC

Chọn C

Câu 9: Cho hình hộp ABCD.A’B’C’D’. Gọi M; N; P; K và H lần lượt là trung điểm của AB; BC; CD; C’D’ và A’D’. Tìm mệnh đề sai?

A. MN // mp(HKD)

B. mp(B’MN) // mp(HKD)

C. DK // mp(MNB’)

D. C’P // mp(NB’D’)

Lời giải:

   + Xét tam giác ABC có M và N lần lượt là trung điểm của AB và BC.

⇒ MN là đường trung bình của tam giác ABC và MN // AC    (1)

   + Tương tự; HK là đường trung bình của tam giác A’D’C’ nên HK // A’C’   (2)

Mà AC // A’C’ ( tính chất của hình hộp)

⇒ MN // HK (*)

Mà HK ⊂ mp(HKD) nên MN // mp(HKD)

⇒ A đúng

   + Hình bình hành ABCD có MP là đường trung bình nên MP // BC và MP = BC

Lại có: BC // B’C’ và BC = B’C’

⇒ MP // B’C’ và MP = B’C’

⇒ Tứ giác MPC’B’ là hình bình hành.

⇒ MB’ // PC’   (3)

   + dễ chứng minh được tứ giác DPC’K là hình bình hành nên DK // PC’  (4)

Từ (3) và (4) suy ra: MB’ // DK   (**)

Mà MB’ ⊂ mp(MNB’) nên DK // mp (MNB’)

⇒ C đúng

   + từ (*) và (**) suy ra: B. mp(B’MN) // mp(HKD).

⇒ B đúng

Chọn D