Cách tìm công thức của số hạng tổng quát cực hay có lời giải - Toán lớp 11

---

Cách tìm công thức của số hạng tổng quát cực hay có lời giải

Với Cách tìm công thức của số hạng tổng quát cực hay có lời giải Toán lớp 11 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tìm công thức của số hạng tổng quát từ đó đạt điểm cao trong bài thi môn Toán lớp 11.

A. Phương pháp giải

• Nếu u_n có dạng u_n = a₁ + a₂ + ... + a_k + .. + a_n thì biến đổi a_k thành hiệu của hai số hạng, dựa vào đó thu gọn u_n .

• Nếu dãy số (u_n) được cho bởi một hệ thức truy hồi, tính vài số hạng đầu của dãy số (chẳng hạn tính u₁; u₂; ... ). Từ đó dự đoán công thức tính un theo n, rồi chứng minh công thức này bằng phương pháp quy nạp. Ngoài ra cũng có thể tính hiệu:

u_{n + 1} − u_n dựa vào đó để tìm công thức tính u_n theo n.

B. Ví dụ minh họa

Ví dụ 1: Cho dãy số có các số hạng đầu là: 4; 8; 12; 16; 20; 24;... Số hạng tổng quát của dãy số này là:

A. u_n = 4n    B. u_n = 2n+ 2    C. u_n = 2n+ 5    D. u_n = 4n+ 2

Hướng dẫn giải:

Ta có:

4 = 4.1 8 = 4.2 12 = 4.3

16 = 4.4 20 = 4.5 24 = 4.6

Suy ra số hạng tổng quát u_n = 4n.

Chọn A .

Ví dụ 2: Cho dãy số có các số hạng đầu là: .Số hạng tổng quát của dãy số này là:

A. u_n = 7n + 7. B. u_n = 7n .

C. u_n = 7n + 1. D. u_n : Không viết được dưới dạng công thức.

Hướng dẫn giải:

Ta có:

8 = 7 . 1 + 1 15 = 7 . 2 + 1 22 = 7 . 3 + 1

29 = 7 . 4 + 1 36 = 7 . 5 + 1

Suy ra số hạng tổng quát u_n = 7n + 1.

Chọn C.

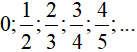
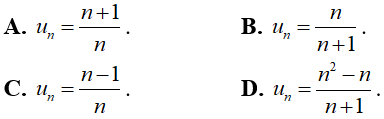
Ví dụ 3: Cho dãy số có các số hạng đầu là: .Số hạng tổng quát của dãy số này là:

Hướng dẫn giải:

Ta có:

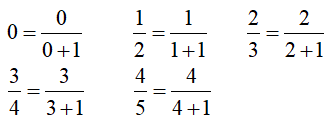
Suy ra số hạng tổng quát của dãy số là: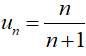

Chọn B.

Ví dụ 4: Cho dãy số có 4 số hạng đầu là: − 1, 3, 19, 53. Hãy tìm một quy luật của dãy số trên và viết số hạng thứ 10 của dãy với quy luật vừa tìm.

A. u₁₀ = 971    B. u₁₀ = 837    C. u₁₀ = 121    D. u₁₀ = 760

Hướng dẫn giải:

Xét dãy (u_n) có dạng: u_n = an³ + bn² + cn + d

Theo giả thiết ta có: u₁ = − 1; u₂ = 3; u₃ = 19 và u₄ = 53

=> hệ phương trình:

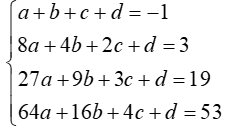
Giải hệ trên ta tìm được: a = 1;b = 0 ; c = −3 và d = 1.

Khi đó; số hạng tổng quát của dãy số là: u_n = n³ − 3n+ 1

Số hạng thứ 10: u₁₀ = 971 .

Chọn A .

Ví dụ 5: Cho dãy số có các số hạng đầu là:0,1; 0,01; 0,001; 0,0001.... Số hạng tổng quát của dãy số này có dạng?

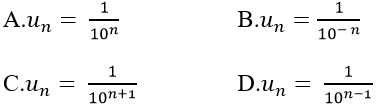
Hướng dẫn giải:

Ta thấy:

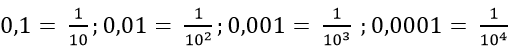
=> Số hạng thứ n là: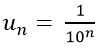

Chọn A.

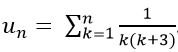
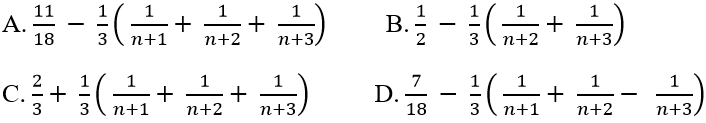
Ví dụ 6: Cho . Xác định công thức tính u_n

Hướng dẫn giải:

Ta có:

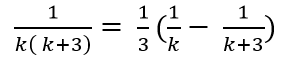
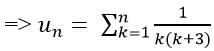
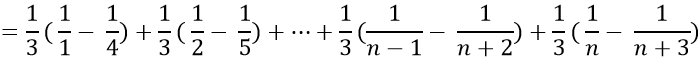
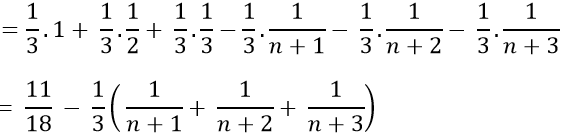
Chọn C.

Ví dụ 7: Cho dãy số có các số hạng đầu là: − 2; 0; 2; 4; 6...Số hạng tổng quát của dãy số này có dạng?

A. u_n = −2n .    B. u_n = − 2 + n .    C. u_n = − 2(n+ 1) .    D.u_n = − 2 + 2(n − 1)

Hướng dẫn giải:

Dãy số là dãy số cách đều có khoảng cách là 2 và số hạng đầu tiên là (−2) nên

u_n = − 2 + 2(n − 1) .

chọn D.

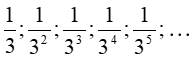
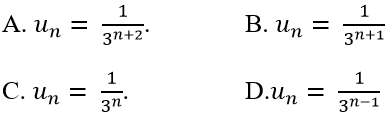
Ví dụ 8: Cho dãy số có các số hạng đầu là: .Số hạng tổng quát của dãy số này là?

Hướng dẫn giải:

Ta có;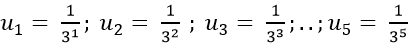

=> Số hạng thứ n của dãy số là: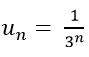

Chọn C.

Ví dụ 9: Cho dãy số (u_n) với 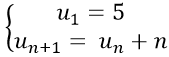.Số hạng tổng quát u_n của dãy số là số hạng nào dưới đây?

Hướng dẫn giải:

Ta có:

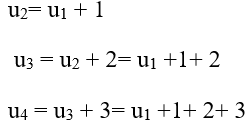
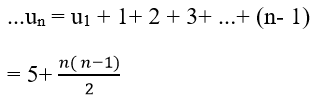
Chọn B.

Ví dụ 10: Cho dãy số (u_n) với 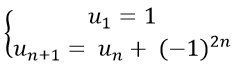. Số hạng tổng quát u_n của dãy số là số hạng nào dưới đây?

A. u_n = 1 + n    B. u_n = n(n + 1)    C. u_n = 1 + (−1)²ⁿ.    D. u_n = n

Hướng dẫn giải:

* Ta có: u_n+1 = u_n + (−1)²ⁿ = u_n + 1 (vì (−1)²ⁿ = ((−1)²)ⁿ = 1

=> u₂ = 2 ; u₃ = 3; u₄ = 4; ...

Dễ dàng dự đoán được: u_n= n.

Thật vậy, ta chứng minh được : u_n = n bằng phương pháp quy nạp như sau:

+ Với n = 1 => u₁ = 1. Vậy (*) đúng với n = 1.

+ Giả sử (*) đúng với mọi n = k ( k ∈ N*), ta có u_k = k.

Ta đi chứng minh (*) cũng đúng với n = k + 1, tức là u_k+1 = k + 1

+ Thật vậy, từ hệ thức xác định dãy số (un ) ta có: u_k+1 = u_k + 1= k+ 1

Vậy (*) đúng với mọi n.

Chọn D.

Ví dụ 11: Cho dãy số (u_n) với 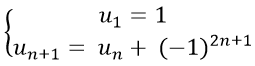. Số hạng tổng quát un của dãy số là số hạng nào dưới đây?

A. u_n = 2 − n    B. không xác định.

C. u_n = 1 − n.    D. u_n = −n với mọi n.

Hướng dẫn giải:

+ Ta có: u₂ = 0; u₃ = −1; u₄ = −2...

Dễ dàng dự đoán được u_n = 2 − n.

+ Thật vậy; với n = 1 ta có: u₁ = 1 ( đúng)

Giả sử với mọi n = k ( k ∈ N*) thì u_k = 2 − k.

Ta chứng minh: u_k+1 = 2 − (k+ 1)

Theo giả thiết ta có: u_{k + 1} = u_k + (−1)^{2k + 1} = 2 − k − 1 = 2 − (k+1)

=> điều phải chứng minh.

Ví dụ 12: Cho dãy số (u_n) với 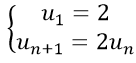.Công thức số hạng tổng quát của dãy số này :

A. u_n = nⁿ⁻¹.    B. u_n = 2ⁿ.

C. u_n = 2ⁿ⁺¹.    D. u_n = 2^{n − 1}

Hướng dẫn giải:

+ Ta có:

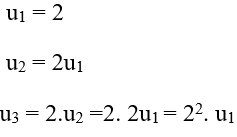
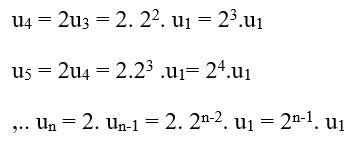
Hay u_n = 2ⁿ (vì u₁ = 2)

Chọn B.

C. Bài tập trắc nghiệm

Câu 1: Cho dãy số có các số hạng đầu là: −1; 1; −1; 1; −1; 1; ...Số hạng tổng quát của dãy số này có dạng

A.u_n = 1     B. u_n = − 1     C. u_n = (−1)n     D. u_n = (−1)ⁿ⁺¹

Lời giải:

Đáp án: C

Ta có thể viết lại các số hạng của dãy như sau:

(−1)¹; (−1)²; (−1)³; (−1)⁴; (−1)⁵; (−1)⁶

=> Số hạng tổng quát của dãy số là u_n = (−1)ⁿ

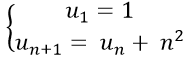
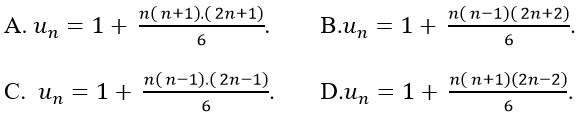
Câu 2: Cho dãy số (u_n) với . Số hạng tổng quát u_n của dãy số là số hạng nào dưới đây?

Lời giải:

Đáp án: C

Ta có:

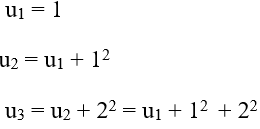
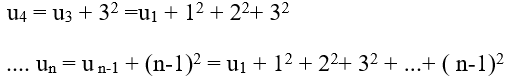
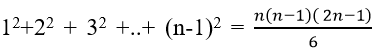
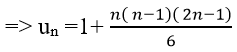
Áp dụng công thức: ( chứng minh bằng phương pháp quy nạp)

Câu 3: Cho dãy số (u_n) với 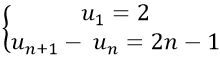. Số hạng tổng quát u_n của dãy số là số hạng nào dưới đây?

A. u_n = 2 + (n−1)².    B. u_n = 2 + n².    C.u_n = 2 + (n+1)².    D. u_n = 2 − (n−1)².

Lời giải:

Đáp án: A

Ta có: u_n+1 − u_n = 2n − 1 suy ra: u_n+1 = u_n + 2n − 1

Theo đầu bài:

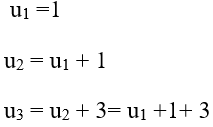
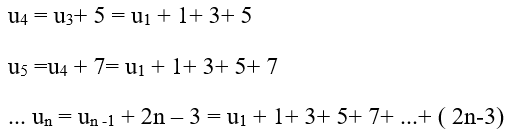
Áp dụng công thức: 1 + 3 + 5 + 7 +...+ (2n − 3) = (n−1)² (chứng minh bằng phương pháp quy nạp)

=>u_n = u₁ + (n−1)² = 2 + (n − 1)²

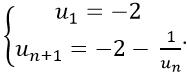
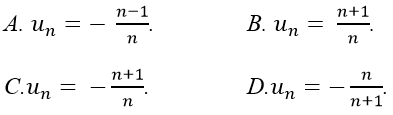
Câu 4: Cho dãy số (u_n) với . Công thức số hạng tổng quát của dãy số này là:

Lời giải:

Đáp án: C

+ Ta có: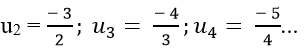

Dự đoán công thức số hạng tổng quát của dãy số là: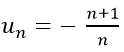

+ Chứng minh công thức trên bằng phương pháp quy nạp:

+ Ta có: 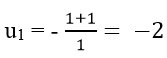nên đúng với n= 1.

Giả sử đúng với n = k (k ∈ N*); tức là: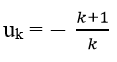

Ta chứng minh đúng với n= k+ 1; tức là chứng minh: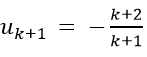

Thật vậy ta có: 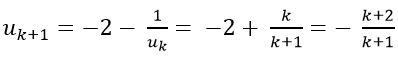( điều phải chứng minh)

Vậy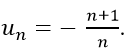

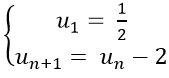
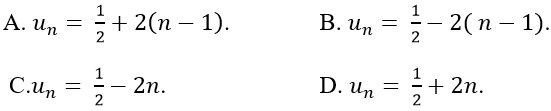
Câu 5: Cho dãy số (u_n) với . Công thức số hạng tổng quát của dãy số này là:

Lời giải:

Đáp án: B

+ Ta có:

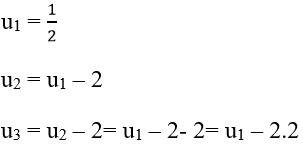
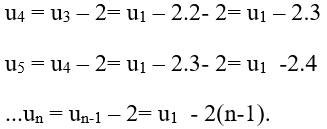
Hay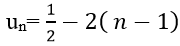

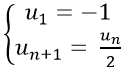
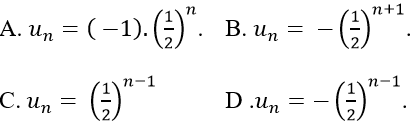
Câu 6: Cho dãy số (u_n) với . Công thức số hạng tổng quát của dãy số này là:

Lời giải:

Đáp án: D

+ Ta có:

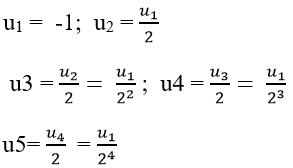
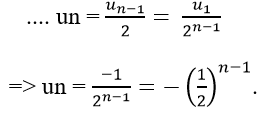
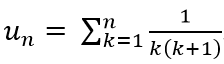
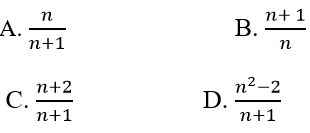
Câu 7: Cho . Xác định công thức tính u_n

Lời giải:

Đáp án: A

+ Ta có:

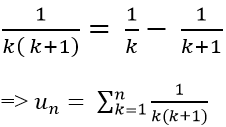
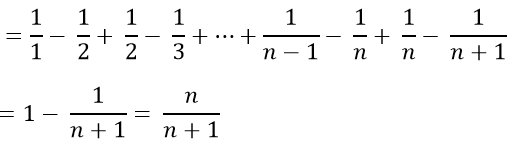
Câu 8: Cho dãy số (u_n) xác định bởi: 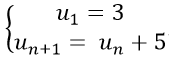. Tìm công thức tính số hạng tổng quát của dãy số.

A. u_n = 3 + 5n    B. u_n = 3 + 5.(n+1)    C. u_n = 5.(n−1)    D. u_n = 3 + 5.(n−1)

Lời giải:

Đáp án: D

Ta có:

u₂ = u₁ + 5 = 8

u₃ = u₂ + 5 = 13

u₄ = u₃ + 5 = 18

u₅ = u₄ + 5 = 23

Từ các số hạng đầu, ta dự đoán số hạng tổng quát un có dạng: u_n = 3 + 5.(n−1) (*) n ≥ 2

+ Ta dùng phương pháp chứng minh quy nạp để chứng minh công thức (*) đúng.

Với n = 2; u₂ = 3+ 5.(2−1) = 8(đúng). Vậy (*) đúng với n = 2

+Giả sử (*) đúng với n = k. Có nghĩa là : u_k = 3+ 5(k−1) (1)

Ta cần chứng minh (*) đúng với n = k+ 1. Có nghĩa là ta phải chứng minh:

u_k+1 = 3 + 5k

Thật vậy từ hệ thức xác định dãy số và theo (1) ta có:

u_k+1 = u_k + 5 = 3 + 5(k − 1) + 5 = 3 + 5k

Vậy (*) đúng khi n = k+ 1.

Kết luận (*) đúng với mọi số nguyên dương n.

Câu 9: Dãy số (u_n) được xác định bằng công thức: 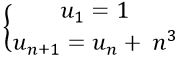. Tính số hạng thứ 100 của dãy số

A. 24502861     B. 24502501     C. 27202501     D. 24547501

Lời giải:

Đáp án: B

+ Trước tiên; ta đi tìm công thức tổng quát của dãy số.

+ Ta có: u_n+1 = u_n + n³ => u_n+1 − u_n = n³

Từ đó suy ra:

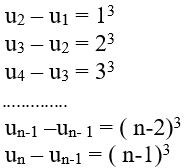
+ Cộng từng vế n đẳng thức trên:

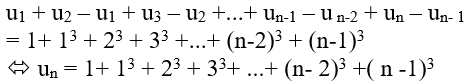
+Bằng phương pháp quy nạp ta chứng minh được:

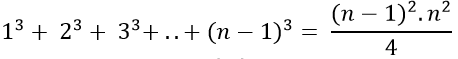
Vậy số hạng tổng quát là: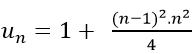

=> Số hạng thứ 100 của dãy số là: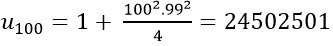

Câu 10: Cho dãy số (u_n) xác định bởi u₁ = 2 và u_n+1 = 5u_n. Tính số hạng thứ 20 của dãy số?

A. 3. 5¹⁰     B. 2.5¹⁹    C. 2 . 5²⁰     D. 3 . 5²⁰

Lời giải:

Đáp án: B

Để tính số hạng thứ 20 của dãy số; ta đi tìm công thức xác định số hạng u_n

+ Ta có: u₂ = 10; u₃ = 50; u₄ = 250; u₅ = 1250; u₆ = 6250

+Ta dự đoán: u_n = 2. 5ⁿ⁻¹ (1) với mọi n ≥ 1. Ta chứng minh bằng phương pháp quy nạp

Với n = 1 ta có: u₁ = 2. 50 = 2 (đúng). Vậy (1) đúng với n = 1.

Giả sử (1) đúng với n = k (k ∈ N*). Có nghĩa là ta có: u_k = 2. 5^k−1

Ta phải chứng minh (1) đúng với n = k+ 1

Có nghĩa ta phải chứng minh: u_k+1 = 2.5^k

Từ hệ thức xác định dãy số (u_n) và giả thiết quy nạp ta có:

u_k+1 = 5u_k = 2. 5^k−1 . 5= 2 . 5^k (đpcm).

=> Số hạng thứ n của dãy số xác định bởi : u_n = 2. 5ⁿ⁻¹

=>Số hạng thứ 20 của dãy số là : u₂₀ = 2.5¹⁹.

Câu 11: Cho dãy số (u_n) xác định bởi u₁ = 3 và u_n+1 = √(1+ u_n²) với n ∈ N*. Tính số hạng thứ 28 của dãy số ?

A. 6     B. 7     C. 8     D. 9

Lời giải:

Đáp án: A

Để tính số hạng thứ 30 của dãy số ta đi tìm công thức xác định số hạng thứ n của dãy số>

+ Ta có:

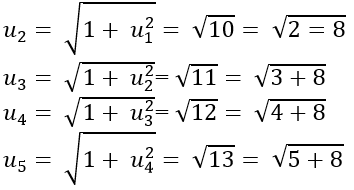
Ta dự đoán : u_n = √(n+8) (1). Ta chứng minh bằng phương pháp quy nạp :

+ Với n = 1 có u₁ = √(1+8) = 3 (đúng). Vậy (1) đúng với n = 1 .

Giả sử (1) đúng với n = k ; k ∈ N* , có nghĩa ta có u_k = √(k+8) (2).

Ta cần chứng minh (1) đúng với n= k + 1. Có nghĩa là ta phải chứng minh:

u_{k + 1} = √(k+9)

Thật vậy từ hệ thức xác định dãy số và theo (2) ta có:

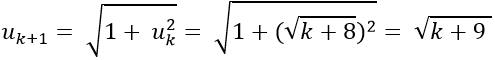
Vậy (1) đúng với n = k + 1.

Kết luận số hạng tổng quát của dãy số là : u_n = √(n+8).

Số hạng thứ 28 của dãy số là : u₂₈= √(28+8) = 6.